نحوه شمارش عدد زیر ریشه نحوه گرفتن ریشه یک عدد چند رقمی

برای محاسبه ریشه دومبدون ماشین حساب، چندین روش وجود دارد.

چگونه ریشه یک عدد را پیدا کنیم - راه 1

• یکی از روش ها فاکتورسازی عددی است که زیر ریشه است. این اجزا در نتیجه ضرب، یک مقدار ریشه را تشکیل می دهند. دقت نتیجه به دست آمده به تعداد زیر ریشه بستگی دارد.
• به عنوان مثال، اگر عدد 1600 را بگیرید و شروع به فاکتورگیری کنید، استدلال به صورت زیر ساخته می شود: این عدد مضربی از 100 است، به این معنی که می توان آن را بر 25 تقسیم کرد. از آنجایی که ریشه عدد 25 استخراج می شود، عدد مربع است و برای محاسبات بعدی مناسب است. هنگام تقسیم، عدد دیگری به دست می آید - 64. این عدد نیز مربع است، بنابراین ریشه به خوبی استخراج می شود. بعد از این محاسبات زیر ریشه می توانید عدد 1600 را به صورت حاصل ضرب 25 و 64 بنویسید.

• یکی از قوانین استخراج ریشه می گوید که ریشه حاصلضرب عوامل برابر عدد است، که از ضرب ریشه هر عامل به دست می آید. این بدان معنی است که: √(25*64) = √25 * √64. اگر ریشه های 25 و 64 را استخراج کنیم عبارت زیر به دست می آید: 5 * 8 = 40. یعنی جذر عدد 1600 برابر با 40 است.
• اما اتفاق می افتد که عدد زیر ریشه به دو عامل تجزیه نمی شود که از آنها کل ریشه استخراج می شود. معمولاً این کار فقط برای یکی از ضرایب ها قابل انجام است. بنابراین، اغلب یافتن پاسخ کاملاً دقیق در چنین معادله ای غیرممکن است.
• در این حالت فقط یک مقدار تقریبی قابل محاسبه است. بنابراین، باید ریشه فاکتور را که یک عدد مربع است، بگیرید. سپس این مقدار در ریشه عدد دوم ضرب می شود که مجذور معادله نیست.
• به نظر می رسد که مثلاً عدد 320 را بگیرید. می توان آن را به 64 و 5 تجزیه کرد. می توانید کل ریشه را از 64 استخراج کنید اما از 5 نه. بنابراین، عبارت به این صورت خواهد بود: √320 = √(64*5) = √64*√5 = 8√5.
• در صورت لزوم می توانید با محاسبه مقدار تقریبی این نتیجه را پیدا کنید
  √5 ≈ 2.236، بنابراین، √320 = 8 * 2.236 = 17.88 ≈ 18.
• همچنین عدد زیر ریشه را می توان به چند عامل اول تجزیه کرد و همان ها را از زیر آن خارج کرد. مثال: √75 = √(5*5*3) ​​= 5√3 ≈ 8.66 ≈ 9.

نحوه پیدا کردن ریشه یک عدد - 2 راه

• راه دیگر تقسیم به یک ستون است. تقسیم مشابه است، اما شما فقط باید به دنبال اعداد مربع باشید، سپس ریشه را از آن استخراج کنید.
• در این صورت عدد مربع را در بالا می نویسیم و در سمت چپ آن را کم می کنیم و ریشه استخراج شده را از پایین.
• حال باید مقدار دوم را دو برابر کرد و از پایین سمت راست به شکل عدد_x_= نوشت. شکاف ها باید با عددی پر شوند که کمتر یا مساوی با مقدار مورد نیاز در سمت چپ باشد - درست مانند تقسیم عادی.
• در صورت لزوم، این نتیجه دوباره از سمت چپ کم می شود. چنین محاسباتی تا رسیدن به نتیجه ادامه دارد. صفرها را نیز می توان تا زمانی که تعداد ارقام اعشاری مورد نظر را بدست آورید اضافه کرد.

ریاضیات زمانی متولد شد که شخص از خود آگاه شد و شروع به قرار دادن خود به عنوان یک واحد مستقل از جهان کرد. میل به اندازه گیری، مقایسه، محاسبه آنچه شما را احاطه کرده است، چیزی است که زیربنای یکی از علوم بنیادی روزگار ما است. در ابتدا، اینها ذرات ریاضیات ابتدایی بودند که اتصال اعداد را با عبارات فیزیکی آنها ممکن می کرد، بعداً نتیجه گیری ها فقط به صورت نظری (به دلیل انتزاعی بودن آنها) ارائه شد، اما پس از مدتی، همانطور که یکی از دانشمندان بیان کرد، " ریاضیات زمانی به سقف پیچیدگی رسید که همه اعداد." مفهوم "ریشه مربع" در زمانی ظاهر شد که به راحتی توسط داده های تجربی پشتیبانی می شد و فراتر از سطح محاسبات بود.

چگونه همه چیز شروع شد

اولین ذکر ریشه، که در حال حاضر به عنوان √ نشان داده می شود، در نوشته های ریاضیدانان بابلی، که پایه و اساس حساب مدرن را پایه گذاری کردند، ثبت شده است. البته، آنها کمی شبیه شکل فعلی بودند - دانشمندان آن سال ها برای اولین بار از قرص های حجیم استفاده کردند. اما در هزاره دوم ق.م. ه. آنها با یک فرمول محاسباتی تقریبی آمدند که نشان می داد چگونه جذر را می توان گرفت. عکس زیر سنگی را نشان می دهد که دانشمندان بابلی فرآیند خروجی √2 را بر روی آن حک کردند و آنقدر درست بود که اختلاف پاسخ فقط در رقم دهم اعشار یافت شد.

علاوه بر این، در صورت نیاز به یافتن ضلع مثلث، از ریشه استفاده می شد، مشروط بر اینکه دو ضلع دیگر مشخص باشند. خوب، هنگام حل معادلات درجه دوم، گریزی از استخراج ریشه نیست.

همراه با آثار بابلی، موضوع مقاله در کار چینی "ریاضیات در نه کتاب" نیز مورد بررسی قرار گرفت و یونانیان باستان به این نتیجه رسیدند که هر عددی که ریشه از آن بدون باقی مانده استخراج نشود، نتیجه غیرمنطقی می دهد. .

منشأ این اصطلاح با نمایش عربی عدد مرتبط است: دانشمندان باستان معتقد بودند که مربع یک عدد دلخواه از ریشه مانند یک گیاه رشد می کند. در لاتین، این کلمه مانند ریشه به نظر می رسد (می توان یک الگو را دنبال کرد - هر چیزی که بار معنایی "ریشه" دارد، همخوان است، چه تربچه یا سیاتیک).

دانشمندان نسل‌های بعدی این ایده را برداشتند و آن را Rx نامیدند. مثلاً در قرن پانزدهم برای اینکه نشان دهند جذر از یک عدد دلخواه a گرفته شده است، R 2 a نوشتند. "تیک" √، آشنا به ظاهر مدرن، تنها در قرن هفدهم به لطف رنه دکارت ظاهر شد.

روزهای ما

از نظر ریاضی، جذر y عدد z است که مربع آن y است. به عبارت دیگر z 2 =y معادل √y=z است. با این حال این تعریففقط برای ریشه حسابی مرتبط است، زیرا بر مقدار غیر منفی عبارت دلالت دارد. به عبارت دیگر √y=z که z بزرگتر یا مساوی 0 است.

به طور کلی که برای تعیین ریشه جبری معتبر است، مقدار عبارت می تواند مثبت یا منفی باشد. بنابراین با توجه به اینکه z 2 =y و (-z) 2 =y داریم: √y=±z یا √y=|z|.

با توجه به این که عشق به ریاضیات تنها با پیشرفت علم افزایش یافته است، مظاهر مختلفی از محبت نسبت به آن وجود دارد که در محاسبات خشک بیان نمی شود. به عنوان مثال، در کنار رویدادهای جالبی مانند روز پی، تعطیلات ریشه مربع نیز جشن گرفته می شود. آنها نه بار در صد سال جشن گرفته می شوند و بر اساس اصل زیر تعیین می شوند: اعدادی که به ترتیب روز و ماه را نشان می دهند باید جذر سال باشند. بنابراین، دفعه بعد این تعطیلات در 4 آوریل 2016 جشن گرفته می شود.

ویژگی های جذر در فیلد R

تقریباً تمام عبارات ریاضی مبنای هندسی دارند، این سرنوشت گذشت و √y که به عنوان ضلع مربع با مساحت y تعریف می شود.

چگونه ریشه یک عدد را پیدا کنیم؟

چندین الگوریتم محاسبه وجود دارد. ساده ترین، اما در عین حال بسیار دست و پا گیر، محاسبه معمولی حسابی است که به شرح زیر است:

1) از عددی که ریشه آن نیاز داریم، اعداد فرد به نوبه خود کم می شوند - تا زمانی که باقیمانده خروجی کمتر از یک تفریق شده یا حتی برابر با صفر شود. تعداد حرکات در نهایت به تعداد مورد نظر تبدیل می شود. برای مثال، محاسبه جذر 25:

عدد فرد بعدی 11 است، باقیمانده: 1<11. Количество ходов - 5, так что корень из 25 равен 5. Вроде все легко и просто, но представьте, что придется вычислять из 18769?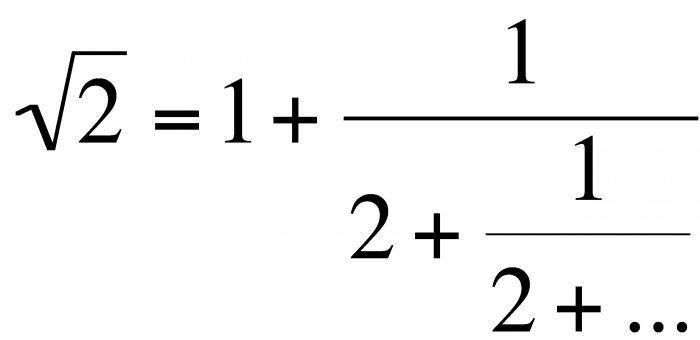

برای چنین مواردی، یک بسط سری تیلور وجود دارد:

√(1+y)=∑((-1) n (2n)!/(1-2n)(n!) 2 (4 n))y n، که در آن n مقادیر از 0 تا

+∞، و |y|≤1.

نمایش گرافیکی تابع z=√y

یک تابع ابتدایی z=√y را در میدان اعداد حقیقی R در نظر بگیرید، جایی که y بزرگتر یا مساوی صفر است. نمودار او به این شکل است: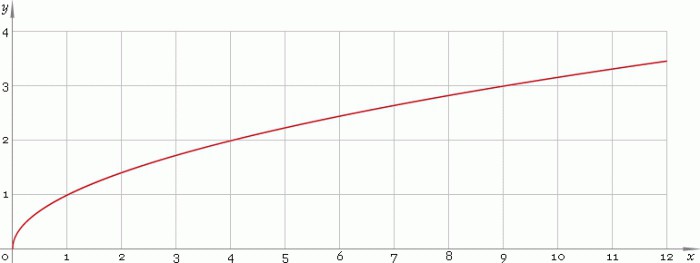

منحنی از مبدأ رشد می کند و لزوماً از نقطه (1؛ 1) عبور می کند.

ویژگی های تابع z=√y در میدان اعداد حقیقی R

1. دامنه تعریف تابع در نظر گرفته شده، فاصله صفر تا بعلاوه بی نهایت است (صفر گنجانده شده است).

2. محدوده مقادیر تابع در نظر گرفته شده، فاصله صفر تا بعلاوه بی نهایت است (صفر دوباره گنجانده شده است).

3. تابع حداقل مقدار (0) را فقط در نقطه (0؛ 0) می گیرد. حداکثر مقدار وجود ندارد.

4. تابع z=√y نه زوج است و نه فرد.

5. تابع z=√y تناوبی نیست.

6. تنها یک نقطه تلاقی نمودار تابع z=√y با محورهای مختصات وجود دارد: (0; 0).

7. نقطه تقاطع نمودار تابع z=√y نیز صفر این تابع است.

8. تابع z=√y پیوسته در حال رشد است.

9. تابع z=√y فقط مقادیر مثبت می گیرد، بنابراین نمودار آن اولین زاویه مختصات را اشغال می کند.

گزینه هایی برای نمایش تابع z=√y

در ریاضیات برای سهولت در محاسبه عبارات پیچیده، گاهی از شکل قدرت نوشتن جذر استفاده می کنند: √y=y 1/2. این گزینه برای مثال برای بالا بردن یک تابع به توان مناسب است: (√y) 4 =(y 1/2) 4 =y 2 . این روش همچنین نمایش خوبی برای تمایز با ادغام است، زیرا به لطف آن ریشه دوم با یک تابع توان معمولی نشان داده می شود.

و در برنامه نویسی جایگزین علامت √ ترکیب حروف sqrt است.

شایان ذکر است که در این منطقه، ریشه مربع تقاضای زیادی دارد، زیرا بخشی از بسیاری از فرمول های هندسی لازم برای محاسبات است. الگوریتم شمارش خود کاملاً پیچیده است و مبتنی بر بازگشت است (عملی که خود را فراخوانی می کند).

جذر در میدان مختلط C

به طور کلی، موضوع این مقاله بود که کشف میدان اعداد مختلط C را تحریک کرد، زیرا ریاضیدانان درگیر مسئله به دست آوردن ریشه درجه زوج از یک عدد منفی بودند. به این ترتیب واحد خیالی i ظاهر شد که با یک ویژگی بسیار جالب مشخص می شود: مربع آن -1 است. با تشکر از این، معادلات درجه دوم و با یک ممیز منفی یک راه حل دریافت کردند. در C، برای جذر، همان خصوصیات مربوط به R است، تنها چیزی که محدودیت های بیان ریشه حذف شده است.

استخراج ریشه از یک عدد بزرگ دوستان عزیز!در این مقاله به شما نشان خواهیم داد که چگونه یک عدد بزرگ را بدون ماشین حساب ریشه بگیرید. این نه تنها برای حل انواع خاصی از مسائل USE ضروری است (چنین مشکلاتی برای حرکت وجود دارد)، بلکه دانستن این تکنیک تحلیلی برای توسعه ریاضی عمومی نیز مطلوب است.

به نظر می رسد که همه چیز ساده است: فاکتورسازی و استخراج. مشکلی نیست. به عنوان مثال، عدد 291600، وقتی بزرگ شود، محصول را نشان می دهد:

محاسبه می کنیم:

یک اما وجود دارد! روش خوب است اگر مقسوم علیه های 2، 3، 4 و غیره به راحتی تعیین شوند. اما اگر عددی که ریشه را از آن استخراج می کنیم حاصل ضرب اعداد اول باشد چه؟ به عنوان مثال، 152881 حاصل ضرب اعداد 17، 17، 23، 23 است. سعی کنید فوراً این مقسوم‌گیرندگان را پیدا کنید.

ماهیت روشی که ما در نظر داریم- این تحلیل محض است ریشه با مهارت انباشته شده به سرعت پیدا می شود. اگر مهارت به کار نرود، اما رویکرد به سادگی درک شود، کمی کندتر است، اما همچنان مصمم است.

بیایید ریشه 190969 را بگیریم.

ابتدا، بیایید تعیین کنیم که نتیجه ما بین چه اعدادی (مضربی از صد) قرار دارد.

بدیهی است که نتیجه ریشه یک عدد معین در محدوده 400 تا 500 قرار دارد.زیرا

400 2 = 160000 و 500 2 = 250000

واقعا:

در وسط، نزدیک به 160000 یا 250000؟

عدد 190969 جایی در وسط است، اما هنوز به 160000 نزدیک تر است. می توانیم نتیجه بگیریم که نتیجه ریشه ما کمتر از 450 خواهد بود. بیایید بررسی کنیم:

در واقع، از 190969 کمتر از 450 است< 202 500.

حالا بیایید عدد 440 را بررسی کنیم:

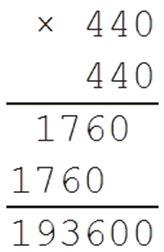
بنابراین نتیجه ما کمتر از 440 است، زیرا 190 969 < 193 600.

بررسی شماره 430:

ما ثابت کرده ایم که نتیجه این ریشه در محدوده 430 تا 440 قرار دارد.

حاصل ضرب اعدادی که به 1 یا 9 ختم می شوند، عددی را به دست می دهد که به 1 ختم می شود. مثلاً 21 ضربدر 21 برابر با 441 است.

حاصل ضرب اعدادی که به 2 یا 8 ختم می شوند، عددی را به دست می دهد که به 4 ختم می شود. مثلاً 18 ضربدر 18 برابر با 324 است.

حاصل ضرب اعدادی که به 5 ختم می شوند، عددی را به دست می دهد که به 5 ختم می شود. مثلاً 25 ضربدر 25 برابر با 625 است.

حاصل ضرب اعدادی که به 4 یا 6 ختم می شوند، عددی به دست می دهد که به 6 ختم می شود. مثلاً 26 ضربدر 26 برابر با 676 است.

حاصل ضرب اعدادی که به 3 یا 7 ختم می شوند، عددی را به دست می دهد که به 9 ختم می شود. مثلاً 17 ضربدر 17 برابر با 289 است.

از آنجایی که عدد 190969 به عدد 9 ختم می شود، پس این محصول یا 433 یا 437 است.

*فقط آنها وقتی مربع شوند می توانند 9 را در پایان بدهند.

بررسی می کنیم:

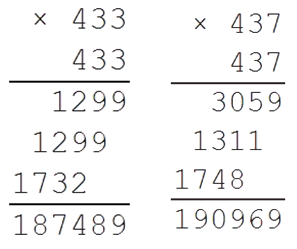
بنابراین نتیجه ریشه 437 خواهد بود.

یعنی به نوعی پاسخ درست را «احساس کردیم».

همانطور که می بینید، حداکثر مورد نیاز انجام 5 عمل در یک ستون است. شاید بلافاصله به اصل مطلب برسید یا فقط سه عمل انجام دهید. همه چیز به این بستگی دارد که چقدر دقیق تخمین اولیه را از عدد انجام می دهید.

ریشه خود را از 148996 استخراج کنید

چنین تمایزی در مسئله به دست می آید:

کشتی موتوری از کنار رودخانه تا مقصد 336 کیلومتر عبور می کند و پس از پارک به نقطه عزیمت باز می گردد. سرعت کشتی را در آب ساکن پیدا کنید، اگر سرعت جریان 5 کیلومتر در ساعت باشد، پارک 10 ساعت طول می کشد و کشتی 48 ساعت پس از خروج از آن به نقطه عزیمت باز می گردد. پاسخ خود را بر حسب کیلومتر بر ساعت بدهید.

مشاهده راه حل

نتیجه ریشه بین اعداد 300 و 400 است:

300 2 =90000 400 2 =160000

در واقع 90000<148996<160000.

ماهیت استدلال بیشتر این است که تعیین کنیم که چگونه عدد 148996 نسبت به این اعداد (فاصله) قرار دارد.

تفاوت ها را محاسبه کنید 148996 - 90000=58996 و 160000 - 148996=11004.

معلوم می شود که 148996 نزدیک (بسیار نزدیکتر) به 160000 است. بنابراین، نتیجه ریشه قطعاً بیشتر از 350 و حتی 360 خواهد بود.

جواب: 386

از نظر عینی، احتمال اینکه شما کار مشابهی دریافت کنید بسیار کم است. اما بگذارید این تکنیک در زرادخانه شما باشد. چیزهای مفید زیادی در انتظار شماست، آن را از دست ندهید!

روش دیگری برای استخراج ریشه از یک عدد بزرگ وجود دارد که آن را الگوریتم اقلیدس می نامند. مزیت آن این است که می توان ریشه را از هر عددی با دقت لازم تا دهم، صدم و ... استخراج کرد. یعنی ریشه ها به صورت اعداد صحیح قابل استخراج نیستند. *این مقاله در آینده به روز رسانی خواهد شد.

با احترام، الکساندر کروتیتسکیخ.

P.S: اگر در مورد سایت در شبکه های اجتماعی بگویید ممنون می شوم.

فصل اول.

استخراج بزرگترین جذر عدد صحیح از یک عدد صحیح داده شده.

170. ملاحظات مقدماتی.

آ)از آنجایی که در این فصل فقط در مورد استخراج ریشه دوم صحبت خواهیم کرد، برای اختصار در این فصل به جای ریشه مربع، به سادگی می گوییم ریشه.

ب)اگر اعداد سری طبیعی را مربع کنیم: 1،2،3،4،5. . . ، سپس جدول مربع های زیر را بدست می آوریم: 1، 4، 9، 16، 25، 36، 49، 64، 81، 100،121،144. .،

بدیهی است که تعداد زیادی اعداد صحیح در این جدول وجود ندارد. البته از چنین اعدادی نمی توان یک ریشه کامل استخراج کرد. بنابراین، برای مثال، اگر می خواهید ریشه یک عدد صحیح را بگیرید. لازم است √4082 را پیدا کنیم، سپس با درک این نیاز به صورت زیر موافقت خواهیم کرد: در صورت امکان، کل ریشه را از 4082 استخراج کنید. اگر نه، پس باید بزرگترین عدد صحیح را پیدا کنیم که مربع آن 4082 است (چنین عددی 63 است، زیرا 63 2 \u003d 3969 و 64 2 \u003d 4090 است).

که در)اگر این عدد کمتر از 100 باشد، ریشه آن در جدول ضرب است. بنابراین √60 می شود 7، زیرا نیم 7 برابر با 49 است که کمتر از 60 است و 8 برابر با 64 است که بزرگتر از 60 است.

171. استخراج ریشه عددی کوچکتر از 10000 ولی بزرگتر از 100.بگذارید لازم باشد √4082 را پیدا کنید. از آنجایی که این عدد کمتر از 10000 است، پس ریشه آن کمتر از √l0 000 = 100 است. از سوی دیگر، این عدد بزرگتر از 100 است. بنابراین ریشه آن بزرگتر از (یا مساوی 10) است. (برای مثال اگر لازم بود √ را پیدا کنید 120 ، سپس اگر چه عدد 120 > 100، اما √ 120 برابر با 10 است زیرا 11 2 = 121.) اما هر عددی که بزرگتر از 10 باشد اما کمتر از 100 باشد دارای 2 رقم است. بنابراین ریشه مورد نظر حاصل جمع است:

ده ها + واحد،

و بنابراین مربع آن باید برابر با مجموع باشد:

این مجموع باید بزرگترین مربع، شامل 4082 باشد.

بیایید بزرگترین آنها، 36، را در نظر بگیریم و فرض کنیم که مربع ده ها ریشه برابر با این بزرگترین مربع باشد. سپس تعداد ده ها در ریشه باید 6 باشد. اکنون بررسی می کنیم که همیشه باید اینطور باشد، یعنی تعداد ده ها ریشه همیشه برابر است با بزرگترین ریشه صحیح صدها عدد ریشه.

در واقع، در مثال ما، تعداد ده ها ریشه نمی تواند بیشتر از 6 باشد، زیرا (7 دسامبر) 2 = 49 صدها، که از 4082 فراتر می رود. اما از 5 دسامبر نمی تواند کمتر از 6 باشد. (با واحدها) کمتر از 6 دس و در ضمن (6 دس) 2 = 36 صد است که کمتر از 4082 است. و چون به دنبال بزرگترین ریشه عدد صحیح هستیم، نباید برای ریشه 5 دس بگیریم، وقتی 6 ده زیاد نیست.

بنابراین، تعداد ده‌ها ریشه یعنی 6 را پیدا کرده‌ایم. این عدد را در سمت راست علامت = می‌نویسیم، به یاد داشته باشید که به معنای ده‌های ریشه است. با بالا بردن آن به مربع، 36 صد به دست می آوریم. این 36 صد را از 40 صد عدد ریشه کم می کنیم و دو رقم دیگر این عدد را از بین می بریم. 482 باقیمانده باید شامل 2 (6 دسامبر) (واحد) + (واحد) 2 باشد. حاصل ضرب (6 دسامبر) (واحد) باید ده باشد. بنابراین، حاصل ضرب مضاعف ده‌ها بر واحدها را باید در ده‌های باقیمانده، یعنی در 48 جست‌وجو کرد (با جدا کردن یک رقم از سمت راست در باقیمانده 48 "2، عدد آنها را به دست خواهیم آورد. که هنوز مشخص نیست). ، سپس باید عدد موجود در 48 را بدست آوریم. بنابراین 48 را بر 12 تقسیم می کنیم.

برای انجام این کار، یک خط عمودی به سمت چپ باقی مانده رسم می کنیم و در پشت آن (از خط یک مکان به سمت چپ برای هدفی که اکنون پیدا می شود حرکت می کنیم) اولین رقم دو برابر شده ریشه را می نویسیم، یعنی 12، و 48 را به آن تقسیم می کنیم در ضریب 4 می گیریم.

با این حال، نمی توان از قبل تضمین داد که عدد 4 را می توان به عنوان واحدهای ریشه در نظر گرفت، زیرا اکنون کل تعداد ده ها باقی مانده را بر 12 تقسیم کرده ایم، در حالی که ممکن است برخی از آنها به حاصل ضرب دو ده ده ها تعلق نداشته باشند. توسط واحدها، اما بخشی از مربع واحدها هستند. بنابراین، عدد 4 ممکن است بزرگ باشد. باید امتحانش کنی بدیهی است که اگر مجموع 2 (6 دسامبر) 4 + 4 2 بیشتر از باقیمانده 482 نباشد، مناسب است.

در نتیجه بلافاصله مجموع هر دو را بدست می آوریم. محصول حاصل 496 بود که بیشتر از باقیمانده 482 است. پس 4 بزرگ است. سپس عدد 3 کوچکتر بعدی را به همین ترتیب تست خواهیم کرد.

مثال ها.

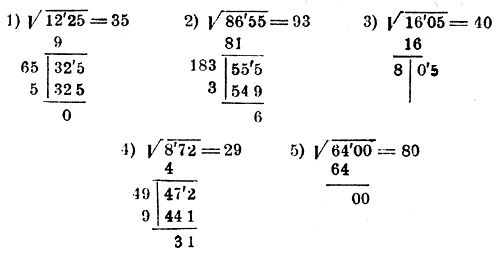
در مثال چهارم وقتی 47 ده باقی مانده را بر 4 تقسیم می کنیم در ضریب 11 می گیریم اما از آنجایی که رقم واحد ریشه نمی تواند یک عدد دو رقمی 11 یا 10 باشد، باید مستقیماً عدد 9 را آزمایش کنیم.

در مثال پنجم، پس از کم کردن 8 از وجه اول مربع، باقیمانده 0 است و وجه بعدی نیز از صفر تشکیل شده است. این نشان می دهد که ریشه مورد نظر فقط از 8 ده تشکیل شده است و بنابراین باید صفر را به جای واحدها قرار داد.

172. استخراج ریشه عددی بزرگتر از 10000. اجازه دهید برای یافتن √35782 مورد نیاز باشد. از آنجایی که عدد رادیکال بزرگتر از 10000 است، پس ریشه آن بزرگتر از √10000 = 100 است و بنابراین از 3 رقم یا بیشتر تشکیل شده است. مهم نیست که از چند رقم تشکیل شده باشد، ما همیشه می توانیم آن را تنها به عنوان مجموع ده ها و واحدها در نظر بگیریم. اگر به عنوان مثال، ریشه 482 بود، می توانیم آن را به عنوان مجموع 48 دس در نظر بگیریم. + 2 واحد سپس مربع ریشه از 3 جمله تشکیل می شود:

(دک.) 2 + 2 (دی

اکنون می‌توانیم دقیقاً به همان روشی که √4082 (در پاراگراف قبل) را پیدا کنیم، استدلال کنیم. تنها تفاوت این خواهد بود که برای یافتن ده ها ریشه 4082 باید ریشه 40 را استخراج کنیم و این کار را می توان با استفاده از جدول ضرب انجام داد. اکنون برای بدست آوردن ده ها√35782 باید ریشه 357 را بگیریم که با استفاده از جدول ضرب نمی توان این کار را انجام داد. اما با ترفندی که در پاراگراف قبل توضیح داده شد، می توانیم √357 را پیدا کنیم، زیرا عدد 357 است.< 10 000. Наибольший целый корень из 357 оказывается 18. Значит, в √3"57"82 должно быть 18 десятков. Чтобы найти единицы, надо из 3"57"82 вычесть квадрат 18 десятков, для чего достаточно вычесть квадрат 18 из 357 сотен и к остатку снести 2 последние цифры подкоренного числа. Остаток от вычитания квадpaта 18 из 357 у нас уже есть: это 33. Значит, для получения остатка от вычитания квадрата 18 дес. из 3"57"82, достаточно к 33 приписать справа цифры 82.

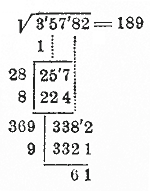
سپس همانطور که هنگام یافتن √4082 انجام دادیم ادامه می دهیم، یعنی: در سمت چپ باقیمانده 3382 یک خط عمودی رسم می کنیم و بعد از آن می نویسیم (یک مکان از خط خارج می شویم) دو برابر تعداد ده ها ریشه یافت شده، یعنی 36. (دوبار 18). در باقیمانده یک رقم سمت راست را جدا می کنیم و تعداد ده ها باقیمانده یعنی 338 را بر 36 تقسیم می کنیم. در ضریب 9 به دست می آید. این عدد را آزمایش می کنیم که آن را به 36 در سمت راست نسبت می دهیم و آن را در آن ضرب کن محصول 3321 بود که کمتر از بقیه است. بنابراین عدد 9 خوب است، آن را در ریشه می نویسیم.

به طور کلی، برای گرفتن جذر هر عدد صحیح، ابتدا باید ریشه صدها آن را گرفت. اگر این عدد بیش از 100 باشد، باید ریشه را از تعداد صدها این صدها، یعنی از ده ها هزار عدد معین جستجو کنید. اگر این عدد بیش از 100 باشد، باید ریشه را از تعداد صدها ده هزار، یعنی از میلیون ها عدد معین و غیره بگیرید.

مثال ها.

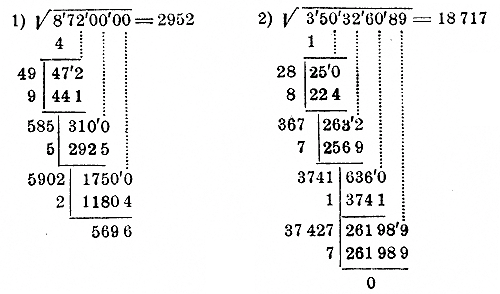
در مثال آخر، با پیدا کردن اولین رقم و کم کردن مربع آن، باقیمانده 0 را بدست می آوریم. 2 رقم بعدی 51 را از بین می بریم. با جدا کردن ده ها، 5 dec به دست می آوریم، در حالی که رقم ریشه دو بار پیدا شده است 6. بنابراین، تقسیم 5 است. با 6، 0 می گیریم، 0 را در ریشه در مکان دوم قرار می دهیم و 2 رقم بعدی را به بقیه حذف می کنیم. 5110 می گیریم. سپس طبق معمول ادامه می دهیم.

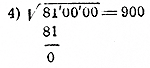
در این مثال، ریشه مورد نظر فقط از 9 صد تشکیل شده است و بنابراین باید به جای ده ها و واحدها، صفر قرار داده شود.

قانون. برای استخراج جذر یک عدد صحیح، آن را از سمت راست به چپ در لبه، با 2 رقم در هر کدام، به جز آخرین رقم که می تواند یک رقمی داشته باشد، بشکنید.
برای پیدا کردن اولین رقم ریشه، جذر وجه اول را بگیرید.
برای یافتن رقم دوم، مجذور رقم اول ریشه از وجه اول کم می شود، وجه دوم به باقی مانده کاهش می یابد و تعداد ده ها عدد حاصل بر دو برابر رقم اول ریشه تقسیم می شود. ; عدد صحیح حاصل تست می شود.
این تست به صورت زیر انجام می شود: پشت خط عمودی (سمت چپ باقیمانده) دو برابر عددی که قبلاً پیدا شده بود از ریشه را می نویسند و به آن در سمت راست، شکل تست، عدد حاصل را پس از این نسبت می دهند. علاوه بر این، عدد در شکل آزمایش ضرب می شود. اگر بعد از ضرب عددی بزرگتر از باقیمانده به دست آید، رقم آزمون خوب نیست و عدد کوچکتر بعدی باید آزمایش شود.
اعداد ریشه زیر نیز با همین روش یافت می شوند.
اگر بعد از تخریب وجه، تعداد ده ها عدد حاصل از مقسوم علیه، یعنی کمتر از دو برابر قسمت یافت شده ریشه باشد، 0 در ریشه قرار می گیرد، وجه بعدی تخریب می شود و اقدام بیشتر ادامه دارد

173. تعداد ارقام ریشه.از در نظر گرفتن فرآیند یافتن ریشه، نتیجه می‌شود که به تعداد چهره‌های 2 رقمی در ریشه، تعداد ارقام در ریشه وجود دارد (ممکن است یک رقم در سمت چپ وجود داشته باشد).

فصل دوم.

استخراج جذر تقریبی از اعداد کامل و کسری .

برای استخراج جذر چند جمله ای ها، به اضافات قسمت دوم § 399 و بعد مراجعه کنید.

174. نشانه های جذر دقیق.جذر دقیق یک عدد معین عددی است که مربع آن دقیقاً برابر عدد داده شده باشد. اجازه دهید برخی از علائم را نشان دهیم که با آنها می توان قضاوت کرد که آیا ریشه دقیق از یک عدد معین استخراج شده است یا خیر:

آ)اگر ریشه عدد صحیح دقیق از یک عدد صحیح معین استخراج نشده باشد (هنگام استخراج باقیمانده به دست می آید)، نمی توان ریشه دقیق کسری را از چنین عددی پیدا کرد، زیرا هر کسری که با یک عدد صحیح برابر نباشد، وقتی در خودش ضرب شود. ، همچنین یک کسری در حاصل ضرب می دهد نه یک عدد صحیح.

ب)از آنجایی که ریشه کسر برابر است با ریشه صورت تقسیم بر ریشه مخرج، اگر کسر تقلیل ناپذیر را نتوان از صورت یا از مخرج استخراج کرد، نمی توان ریشه دقیق آن را یافت. به عنوان مثال، ریشه دقیق را نمی توان از کسرهای 4/5، 8/9 و 11/15 استخراج کرد، زیرا در کسر اول نمی توان آن را از مخرج استخراج کرد، در کسر دوم - از صورت و در سوم - نه از کسر از صورت و نه از مخرج.

از چنین اعدادی که استخراج ریشه دقیق از آنها غیرممکن است، فقط می توان ریشه های تقریبی را استخراج کرد.

175. ریشه تقریبی تا 1. جذر تقریبی تا 1 از یک عدد معین (عدد صحیح یا کسری - مهم نیست) یک عدد صحیح است که دو شرط زیر را برآورده می کند:

1) مربع این عدد از عدد داده شده بزرگتر نباشد. 2) اما مجذور این عدد 1 بیشتر شده از عدد داده شده بزرگتر است. به عبارت دیگر، جذر تقریبی تا 1، بزرگترین جذر صحیح یک عدد معین است، یعنی ریشه ای که در فصل قبل یاد گرفتیم پیدا کنیم. این ریشه را تقریبی تا 1 می نامند، زیرا برای به دست آوردن یک ریشه دقیق، باید کسری کمتر از 1 به این ریشه تقریبی اضافه شود، بنابراین اگر به جای یک ریشه دقیق مجهول، این ریشه تقریبی را بگیریم، خطای کمتر از 1

قانون. برای استخراج یک جذر تقریبی با دقت 1، باید بزرگترین ریشه صحیح قسمت صحیح یک عدد معین را استخراج کنید.

عددی که طبق این قانون یافت می‌شود یک ریشه تقریبی با یک نقطه ضعف است، زیرا مقداری کسری (کمتر از 1) به ریشه دقیق ندارد. اگر این ریشه را 1 افزایش دهیم، عدد دیگری به دست می آید که در آن مقداری بیش از ریشه دقیق وجود دارد و این مازاد کمتر از 1 است. یک مازاد. (نام‌های «با کمبود» یا «با زیاده‌روی» در برخی از کتاب‌های ریاضی با برخی معادل‌های دیگر جایگزین می‌شوند: «با کمبود» یا «با زیاده‌روی».)

176. ریشه تقریبی با دقت 1/10. اجازه دهید برای یافتن √2.35104 تا 1/10 مورد نیاز باشد. این به این معنی است که باید چنین کسر اعشاری را پیدا کرد که از واحدهای کامل و دهم تشکیل شده باشد و دو شرط زیر را برآورده کند:

1) مربع این کسر از 2.35104 تجاوز نمی کند، اما 2) اگر آن را 1/10 افزایش دهیم، مجذور این کسر افزایش یافته از 2.35104 بیشتر می شود.

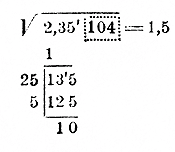
برای یافتن چنین کسری، ابتدا یک ریشه تقریبی تا 1 پیدا می کنیم، یعنی ریشه را فقط از عدد صحیح 2 استخراج می کنیم. 1 می گیریم (و باقیمانده 1 است). عدد 1 را در ریشه می نویسیم و بعد از آن کاما می گذاریم. اکنون به دنبال عدد دهم خواهیم بود. برای این کار، رقم 35 را تا باقیمانده 1 در سمت راست ویرگول حذف می کنیم و استخراج را به گونه ای ادامه می دهیم که گویی ریشه را از عدد صحیح 235 استخراج می کنیم. عدد حاصل را در ریشه به جای عدد 5 می نویسیم. دهمین ما به ارقام باقی مانده از عدد رادیکال (104) نیازی نداریم. اینکه عدد حاصل 1.5 در واقع یک ریشه تقریبی با دقت 1/10 خواهد بود از موارد زیر مشهود است. اگر بخواهیم بزرگترین ریشه عدد صحیح 235 را با دقت 1 پیدا کنیم، 15 به دست می آید.

15 2 < 235، اما 16 2 > 235.

با تقسیم همه این اعداد بر 100 به دست می آید:

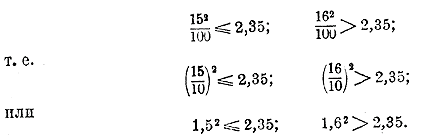
یعنی عدد 1.5 همان کسر اعشاری است که با دقت 1/10 آن را ریشه تقریبی نامیدیم.

همچنین با این روش ریشه های تقریبی زیر را با دقت 0.1 پیدا می کنیم:

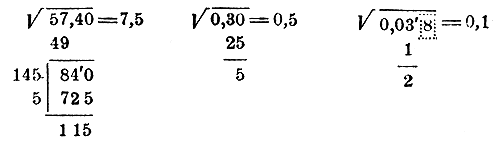
177. جذر تقریبی با دقت 1/100 تا 1/1000 و غیره.

اجازه دهید برای پیدا کردن یک عدد تقریبی √248 با دقت 1/100 لازم باشد. این به این معنی است: برای یافتن کسری اعشاری که از اعداد صحیح، دهم و صدم تشکیل شده باشد و دو شرط را برآورده کند:

1) مربع آن از 248 تجاوز نمی کند، اما 2) اگر این کسر را 1/100 افزایش دهیم، مربع این کسر افزایش یافته از 248 بیشتر می شود.

ما چنین کسری را در دنباله زیر خواهیم یافت: ابتدا یک عدد صحیح، سپس رقم دهم و سپس رقم صدم را پیدا می کنیم. جذر یک عدد صحیح 15 ​​عدد صحیح خواهد بود. برای به دست آوردن عدد دهم، همانطور که دیدیم، باید به 23 باقیمانده 2 رقم دیگر در سمت راست نقطه اعشار پایین بیاوریم. در مثال ما، این اعداد اصلا وجود ندارند، ما صفرها را به جای آنها قرار می دهیم. با اختصاص دادن آنها به باقی مانده و ادامه عمل به گونه ای که انگار داریم ریشه عدد صحیح 24800 را پیدا می کنیم، رقم دهم 7 را می یابیم. باقی مانده است که رقم صدم را پیدا کنیم. برای این کار 2 صفر دیگر به 151 باقی مانده اضافه می کنیم و استخراج را ادامه می دهیم، مثل اینکه داریم ریشه عدد صحیح 2480000 را پیدا می کنیم 15.74 به دست می آید. اینکه این عدد واقعاً ریشه تقریبی 248 تا 1/100 است، از موارد زیر مشهود است. اگر بخواهیم بزرگترین جذر عدد صحیح را از 2,480,000 پیدا کنیم، 1574 بدست می آید. به معنای:

1574 2 < 2,480,000 اما 1575 2 > 2,480,000.

با تقسیم همه اعداد بر 10000 (= 100 2)، به دست می آید:

بنابراین 15.74 آن کسر اعشاری است که ما آن را با دقت 1/100 از 248 ریشه تقریبی نامیدیم.

با استفاده از این تکنیک برای یافتن ریشه تقریبی با دقت 1/1000 تا 1/10000 و غیره به موارد زیر پی می بریم.

قانون. برای استخراج از یک عدد صحیح داده شده یا از یک کسر اعشاری یک ریشه تقریبی با دقت 1/10 تا 1/100 تا 1/100 و غیره، ابتدا یک ریشه تقریبی با دقت 1 پیدا کنید و ریشه را از عدد صحیح (اگر نه، در مورد ریشه 0 عدد صحیح می نویسند).

سپس عدد دهم را پیدا کنید. برای انجام این کار، 2 رقم از عدد رادیکال سمت راست نقطه اعشار را به باقی مانده پایین می آورند (اگر وجود نداشته باشد، دو صفر به باقی مانده نسبت داده می شود) و استخراج را به همان ترتیب ادامه می دهند. هنگام استخراج ریشه از یک عدد صحیح انجام می شود. رقم به دست آمده در ریشه به جای دهم نوشته می شود.

سپس عدد صدم را پیدا کنید. برای انجام این کار، دو عدد دوباره به سمت باقی مانده، به سمت راست آنهایی که اخیراً تخریب شده اند و غیره تخریب می شوند.

بنابراین، هنگام استخراج ریشه از یک عدد صحیح با کسری اعشاری، لازم است که بر روی صورت های 2 رقمی هر کدام، با شروع از کاما، هم به سمت چپ (در قسمت صحیح عدد) و هم به سمت راست تقسیم شود ( در قسمت کسری).

مثال ها.

1) تا 1/100 ریشه را پیدا کنید: a) √2; ب) √0.3;

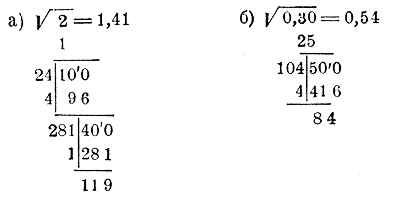
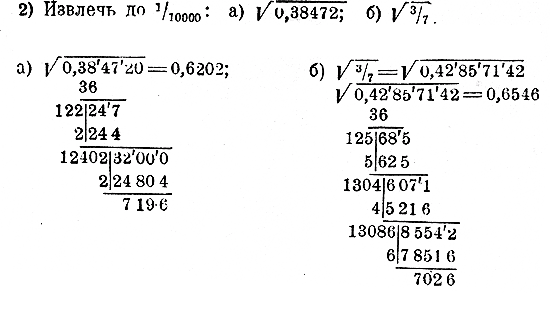
در آخرین مثال، 3/7 را با محاسبه 8 رقم اعشار به اعشار تبدیل کردیم تا 4 وجه مورد نیاز برای یافتن 4 رقم اعشار ریشه را تشکیل دهیم.

178. شرح جدول جذر.در پایان این کتاب جدولی از ریشه های مربع با چهار رقم محاسبه شده است. با استفاده از این جدول، می توانید به سرعت جذر یک عدد صحیح (یا کسر اعشاری) را که بیش از چهار رقم بیان می شود، پیدا کنید. قبل از توضیح نحوه چیدمان این جدول، توجه داشته باشیم که همیشه می‌توانیم اولین رقم معنی‌دار ریشه مورد نظر را بدون کمک جداول با یک نگاه به شماره ریشه پیدا کنیم. ما همچنین می توانیم به راحتی تعیین کنیم که کدام رقم اعشاری به معنای رقم اول ریشه است و بنابراین، در کجای ریشه، زمانی که ارقام آن را پیدا می کنیم، باید یک کاما قرار دهیم. در اینجا چند نمونه آورده شده است:

1) √5"27,3 . رقم اول 2 خواهد بود، زیرا سمت چپ عدد ریشه 5 است. و ریشه 5 برابر 2 است. علاوه بر این، از آنجایی که در قسمت صحیح تعداد رادیکال همه وجوه فقط 2 وجود دارد، پس قسمت صحیح ریشه مورد نظر باید 2 رقم داشته باشد و بنابراین رقم اول آن 2 باید به معنای ده ها.

2) √9.041. بدیهی است که در این ریشه، رقم اول 3 واحد ساده خواهد بود.

3) √0.00"83"4 . اولین رقم معنادار 9 است، زیرا وجهی که برای بدست آوردن اولین رقم مهم باید ریشه از آن استخراج شود 83 است و ریشه 83 9 است. از آنجایی که در عدد مورد نظر نه اعداد صحیح و نه دهم وجود خواهد داشت، رقم اول 9 باید به معنای صدم باشد.

4) √0.73 "85. اولین رقم قابل توجه 8 دهم است.

5) √0.00 "00" 35 "7. اولین رقم قابل توجه 5 هزارم خواهد بود.

اجازه دهید یک نکته دیگر را بیان کنیم. فرض کنید که لازم است ریشه از چنین عددی استخراج شود که پس از کنار گذاشتن عدد اشغال شده در آن، با یک سری اعداد به تصویر کشیده می شود: 5681. این ریشه می تواند یکی از موارد زیر باشد:

اگر ریشه هایی را که زیر آنها خط کشیدیم با یک خط بگیریم، همه آنها با همان سری اعداد بیان می شوند، دقیقاً اعدادی که با استخراج ریشه از 5681 به دست می آیند (اینها اعداد 7، 5، 3، 7 خواهند بود. ). دلیل این امر این است که وجه هایی که هنگام یافتن ارقام ریشه باید به آنها تقسیم شود، در همه این مثال ها یکسان خواهد بود، بنابراین ارقام هر ریشه یکسان خواهد بود (فقط موقعیت کاما). البته متفاوت خواهد بود). به همین ترتیب، در تمام ریشه هایی که با دو خط زیر آنها خط کشیده ایم، باید اعداد یکسانی بدست آید، دقیقاً آنهایی که √568.1 را بیان می کنند (این اعداد 2، 3، 8، 3 خواهند بود) و به همین دلیل. بنابراین، ارقام ریشه ها از اعداد نشان داده شده (با کنار گذاشتن کاما) توسط همان سری ارقام 5681 از نوع دوگانه (و فقط دو برابری) خواهند بود: یا این یک سری از 7، 5، 3، 7 است، یا یک سری از 2، 3، 8، 3. همین را، بدیهی است، می توان در مورد هر سری از ارقام دیگر نیز گفت. بنابراین، همانطور که اکنون خواهیم دید، در جدول، هر ردیف از ارقام عدد رادیکال با 2 ردیف رقم برای ریشه ها مطابقت دارد.

اکنون می توانیم ساختار جدول و نحوه استفاده از آن را توضیح دهیم. برای وضوح بیشتر، ابتدای صفحه اول جدول را در اینجا به تصویر کشیده ایم.

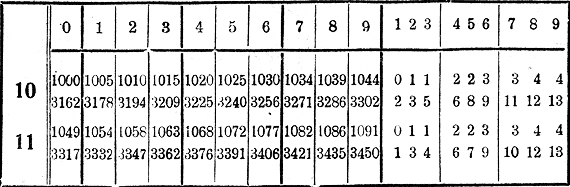
این جدول چندین صفحه را شامل می شود. روی هر کدام از آنها در ستون اول سمت چپ اعداد 10، 11، 12 ... (تا 99) قرار داده شده است. این اعداد بیانگر 2 رقم اول عددی است که از آن جذر جذر می شود. در خط افقی بالا (و همچنین در پایین) اعداد: 0، 1، 2، 3 ... 9 وجود دارد که رقم سوم این عدد است و سپس در سمت راست اعداد 1، 2 قرار دارند. ، 3. . . 9 که نشان دهنده چهارمین رقم این عدد است. در تمام خطوط افقی دیگر، 2 عدد چهار رقمی قرار داده شده است که ریشه های مربع اعداد مربوطه را بیان می کند.

اجازه دهید برای پیدا کردن ریشه دوم برخی از اعداد، اعداد صحیح یا بیان شده به صورت کسری اعشاری لازم باشد. اول از همه، بدون کمک جداول اولین رقم ریشه و دسته آن را می یابیم. سپس کاما را در عدد داده شده در صورت وجود کنار می گذاریم. ابتدا فرض کنید پس از حذف کاما، مثلاً فقط 3 رقم باقی می ماند. 114. در جداول در سمت چپ ترین ستون، 2 رقم اول یعنی 11 را پیدا می کنیم و از آنها در امتداد خط افقی به سمت راست حرکت می کنیم تا به ستون عمودی برسیم که در بالا (و پایین) آن رقم 3 است. از عدد، یعنی 4. در این مکان دو عدد چهار رقمی پیدا می کنیم: 1068 و 3376. کدام یک از این دو عدد را باید گرفت و در کجا کاما گذاشت، این با رقم اول ریشه مشخص می شود و تخلیه آن، که قبلاً پیدا کردیم. بنابراین، اگر باید √0.11 "4 را پیدا کنید، اولین رقم ریشه 3 دهم است، و بنابراین باید 0.3376 را برای ریشه بگیریم. اگر لازم بود √1.14 را پیدا کنید، اولین رقم ریشه خواهد بود. 1 باشد، و سپس 1.068 را می گیریم.

بنابراین ما به راحتی می توانیم پیدا کنیم:

√5.30 = 2.302; √7"18 = 26.80؛ √0.91"6 = 0.9571 و غیره.

اکنون فرض کنیم که لازم است ریشه عددی را که با 4 رقم بیان شده است (با دور انداختن کاما) پیدا کنیم، برای مثال √7 "45.6. با توجه به اینکه رقم اول ریشه 2 ده است، برای عدد پیدا می کنیم. 745، همانطور که اکنون توضیح داده شد، اعداد 2729 (فقط با انگشت متوجه این عدد می شویم، اما آن را یادداشت نمی کنیم.) سپس از این عدد به سمت راست حرکت می کنیم تا در سمت راست جدول (پشت) آخرین خط پررنگ) با ستون عمودی روبرو می شویم که در بالای (و پایین) رقم چهارم این عدد یعنی عدد 6 مشخص شده است و عدد 1 را در آنجا پیدا می کنیم. این اصلاحی است که باید اعمال شود (در قسمت ذهن) به عدد 2729 که قبلاً پیدا شده بود، 2730 می گیریم. این عدد را می نویسیم و در آن در جای مناسب کاما می گذاریم: 27.30.

به این ترتیب به عنوان مثال می یابیم:

√44.37 = 6.661; √4.437 = 2.107; √0.04"437 \u003d 0.2107 و غیره

اگر عدد رادیکال فقط با یک یا دو رقم بیان شود، می توانیم فرض کنیم که بعد از این ارقام یک یا دو صفر وجود دارد و سپس همانطور که برای عدد سه رقمی توضیح داده شد ادامه دهیم. به عنوان مثال √2.7 = √2.70 =1.643; √0.13 \u003d √0.13 "0 \u003d 0.3606 و غیره.

در نهایت، اگر عدد رادیکال با بیش از 4 رقم بیان شود، فقط 4 رقم اول را می گیریم و بقیه را حذف می کنیم و برای کاهش خطا، اگر اولین رقم حذف شده 5 یا بیشتر از 5 باشد، سپس چهارمین ارقام حفظ شده را l افزایش می دهیم. بنابراین:

√357,8| 3 | = 18,91; √0,49"35|7 | = 0.7025; و غیره.

اظهار نظر. جداول جذر تقریبی را نشان می دهد، گاهی با کمبود، گاهی اوقات با اضافه، یعنی یکی از این ریشه های تقریبی که به ریشه دقیق نزدیکتر می شود.

179. استخراج ریشه های مربع از کسرهای معمولی.جذر دقیق یک کسر تقلیل ناپذیر را تنها زمانی می توان استخراج کرد که هر دو عبارت کسر مربع دقیق باشند. در این صورت کافی است ریشه را از صورت و مخرج به طور جداگانه استخراج کنید، به عنوان مثال:

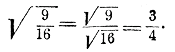
جذر تقریبی یک کسر معمولی با مقداری دقت اعشاری را می توان به راحتی پیدا کرد اگر ابتدا کسر معمولی را به اعشار تبدیل کنیم و در این کسری تعداد ارقام اعشاری بعد از اعشار را محاسبه کنیم که دو برابر تعداد اعشار خواهد بود. در ریشه مورد نظر قرار می گیرد.

با این حال، شما می توانید در غیر این صورت انجام دهید. بیایید این را با مثال زیر توضیح دهیم:

√ 5/24 تقریبی را پیدا کنید

بیایید مخرج را یک مربع دقیق بسازیم. برای این کار کافی است هر دو عبارت کسر را در مخرج 24 ضرب کنیم. اما در این مثال، شما می توانید به طور دیگری انجام دهید. ما 24 را به ضرایب اول تجزیه می کنیم: 24 \u003d 2 2 2 3. از این تجزیه می توان دریافت که اگر 24 در 2 و دیگری در 3 ضرب شود، در حاصل ضرب هر عامل اول به تعداد زوج تکرار می شود. و بنابراین، مخرج به یک مربع تبدیل می شود:

باقی مانده است که √30 را با کمی دقت محاسبه کرده و نتیجه را بر 12 تقسیم کنیم. در این صورت باید در نظر داشت که کسری که درجه دقت را نشان می دهد نیز از تقسیم بر 12 کاهش می یابد. بنابراین، اگر √30 را با دقت 1/10 پیدا کنیم و حاصل را بر 12 تقسیم کنیم، ریشه تقریبی کسری 5/24 را با دقت 1/120 به دست می آوریم (یعنی 54/120 و 55/120)

فصل سه.

نمودار تابعx = √ y .

180. تابع معکوس.اجازه دهید معادله ای وجود داشته باشد که تعریف کند در به عنوان تابعی از ایکس مثلاً این: y = x 2 . می توان گفت که نه تنها تعیین کننده است در به عنوان تابعی از ایکس ، بلکه برعکس، تعیین می کند ایکس به عنوان تابعی از در ، هر چند به صورت ضمنی. برای اینکه این تابع واضح باشد، باید این معادله را حل کنیم ایکس ، گرفتن در برای یک عدد شناخته شده؛ بنابراین، از معادله ای که گرفته ایم، به این نتیجه می رسیم: y = x 2 .

عبارت جبری که برای x پس از حل معادله ای که y را تابعی از x تعریف می کند به دست می آید تابع معکوس آن چیزی است که y را تعریف می کند.

بنابراین تابع x = √ y تابع معکوس y = x 2 . اگر طبق معمول، متغیر مستقل مشخص شود ایکس ، و وابسته در ، سپس می توانیم تابع معکوس بدست آمده را به صورت زیر بیان کنیم: y = √x . بنابراین، برای به دست آوردن تابعی که معکوس با یک داده (مستقیم) است، لازم است از معادله ای که این تابع داده شده را تعریف می کند، استخراج شود. ایکس بسته به y و در عبارت حاصل جایگزین کنید y بر روی ایکس ، آ ایکس بر روی y .

181. نمودار یک تابع y = √x . این تابع با مقدار منفی امکان پذیر نیست ایکس ، اما می توان آن را (با هر دقتی) برای هر مقدار مثبت محاسبه کرد ایکس و برای هر یک از این مقادیر، تابع دو مقدار متفاوت با مقدار مطلق یکسان، اما با علائم مخالف دریافت می کند. اگر آشناست √ ما فقط مقدار حسابی جذر را نشان می دهیم، سپس این دو مقدار تابع را می توان به صورت زیر بیان کرد: y= ± √ x برای رسم این تابع، ابتدا باید جدولی از مقادیر آن ایجاد کنید. ساده ترین راه برای کامپایل این جدول از جدول مقادیر تابع مستقیم است:

y = x 2 .

ایکس

y

اگر مقادیر در را به عنوان ارزش ها در نظر بگیرید ایکس ، و بالعکس:

y= ± √ x

با قرار دادن تمام این مقادیر در نقاشی، نمودار زیر را دریافت می کنیم.

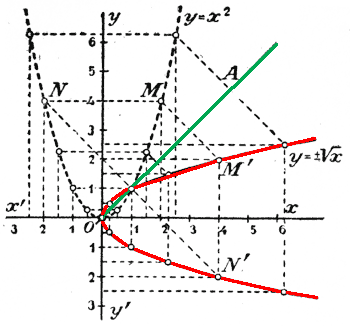
در همان نقاشی (خط چین) و نمودار تابع مستقیم را به تصویر کشیدیم y = x 2 . بیایید این دو نمودار را با هم مقایسه کنیم.

182. رابطه بین نمودارهای توابع مستقیم و معکوس.برای تهیه جدولی از مقادیر تابع معکوس y= ± √ x گرفتیم برای ایکس اعدادی که در جدول تابع مستقیم قرار دارند y = x 2 به عنوان ارزش برای در ، و برای در آن اعداد را گرفت. که در این جدول مقادیر مربوط به آن بودند ایکس . از این نتیجه می شود که هر دو نمودار یکسان هستند، فقط نمودار تابع مستقیم نسبت به محور قرار دارد. در - نحوه قرار گرفتن نمودار تابع معکوس نسبت به محور ایکس - ov. در نتیجه اگر نقاشی را حول یک خط مستقیم تا کنیم OA نصف کردن یک زاویه قائمه xOy ، به طوری که بخشی از نقاشی حاوی نیم محور است OU ، روی قسمتی که شامل نیم محور است افتاد اوه ، سپس OU سازگار با اوه ، تمام بخش ها OU همزمان با تقسیمات اوه ، و نقاط سهمی y = x 2 منطبق با نقاط مربوطه در نمودار y= ± √ x . مثلا نقطه ها م و ن ، که دستور آن 4 ، و آبسیسا 2 و - 2 ، منطبق با نقاط م" و N" ، که آبسیسه 4 ، و احکام 2 و - 2 . اگر این نقاط منطبق باشند، این بدان معنی است که خطوط MM" و NN" عمود بر OAو این خط مستقیم را به نصف تقسیم کنید. همین امر را می توان برای سایر نکات مرتبط در هر دو نمودار گفت.

بنابراین، نمودار تابع معکوس باید با نمودار تابع مستقیم یکسان باشد، اما این نمودارها به طور متفاوتی قرار دارند، یعنی به صورت متقارن با یکدیگر نسبت به نیمساز زاویه قرار دارند. هوی . می توان گفت که نمودار تابع معکوس انعکاسی (مانند یک آینه) از نمودار تابع مستقیم نسبت به نیمساز زاویه است. هوی .

22 دسامبر 2010، 1:13

روزی روزگاری، خیلی وقت پیش، زمانی که کلاس هشتم بودم، معلمم در یک دایره نشان داد که چگونه می توان ریشه های مربع را در یک ستون استخراج کرد. می توانید ریشه را با دقت دلخواه محاسبه کنید، هر تعداد رقمی را که دوست دارید در نماد اعشاری آن پیدا کنید، حتی اگر غیرمنطقی باشد. الگوریتم به خاطر سپرده شد، اما سؤالات باقی ماند. معلوم نبود این روش از کجا آمده و چرا نتیجه درستی می دهد. این در کتاب ها نبود، یا شاید من فقط به دنبال کتاب های اشتباهی بودم. در نتیجه، مانند بسیاری از چیزهایی که امروز می‌دانم و می‌توانم انجام دهم، خودم آن‌ها را مطرح کردم. من دانش خود را در اینجا به اشتراک می گذارم. به هر حال، من هنوز نمی دانم که منطق الگوریتم کجا آمده است)))

بنابراین، ابتدا با استفاده از یک مثال به شما می گویم "چگونه سیستم کار می کند" و سپس توضیح می دهم که چرا واقعاً کار می کند.

بیایید یک عدد بگیریم (عدد "از سقف" گرفته شده است، فقط به ذهنم آمد).

1. ما اعداد آن را به جفت تقسیم می کنیم: آنهایی که در سمت چپ نقطه اعشار قرار دارند، دو را از راست به چپ گروه بندی می کنیم، و آنهایی که به سمت راست هستند - دو نفر از چپ به راست. ما گرفتیم .

2. ما جذر را از اولین گروه از ارقام سمت چپ استخراج می کنیم - در مورد ما اینطور است (معلوم است که ممکن است ریشه دقیق استخراج نشود، عددی را می گیریم که مربع آن تا حد امکان به عدد ما نزدیک است. گروه اول ارقام، اما از آن تجاوز نمی کند). در مورد ما، این یک عدد خواهد بود. ما در پاسخ می نویسیم - این بالاترین رقم ریشه است.

3. عددی را که قبلاً در پاسخ وجود دارد - این است - مربع می کنیم و از اولین گروه اعداد سمت چپ - از عدد کم می کنیم. در مورد ما، باقی می ماند

4. گروه دو عدد زیر را به سمت راست نسبت می دهیم: . عددی که قبلا در پاسخ وجود دارد ضرب شده است، به دست می آوریم.

5. حالا با دقت تماشا کن باید یک رقم را به عدد سمت راست اضافه کنیم و عدد را در همان رقم اختصاص داده شده ضرب کنیم. نتیجه باید تا حد ممکن نزدیک باشد، اما باز هم بیشتر از این عدد نباشد. در مورد ما، این یک عدد خواهد بود، ما آن را در پاسخ در کنار، در سمت راست می نویسیم. این رقم بعدی در نماد اعشاری برای جذر ما است.

6. با تفریق محصول از دریافت می کنیم.

7. سپس عملیات آشنا را تکرار می کنیم: گروه بعدی ارقام را به سمت راست اختصاص می دهیم، در ضرب می کنیم، یک رقم را به سمت راست به عدد حاصل اختصاص می دهیم، به طوری که وقتی در آن ضرب می شود، عددی کوچکتر به دست می آوریم، اما نزدیکترین به آن - این عدد است - رقم بعدی در نماد اعشاری ریشه.

محاسبات به صورت زیر نوشته خواهد شد:

Title="(!LANG:\begin(tabular)( [ایمیل محافظت شده]{} [ایمیل محافظت شده]{} [ایمیل محافظت شده]{} [ایمیل محافظت شده]{} [ایمیل محافظت شده]()ج)
\multicolumn(5)(l)($\sqrt(5 ` 67` 89.32` 1)$)&$=238.30\ldots$\\
\ \ 4 & & & & &\\
\cline (1-3)
\ \ 1 & 67 & & & &\\
\ \ 1 & 29 & & & &\\
\cline (1-4)
\ \ & 38 & 89 & & &\\
\ \ & 37 & 44 & & &\\
\cline (2-5)
\ \ & 1 & 45 & 32 & &\\
\ \ & 1 & 42 & 89 & &\\
\cline (2-5)
\ \ & & 2 & 43 & 1000 &\\
\ \ & & 2 & 38 & 3025 &\\
\cline (3-5)
\ \ & & & 4 & 7975 &\\
\ \ & & & & $\ldots$ &
\پایان (جدولی)
\begin(آرایه)(l)

468\cdot8=3744،\\
4763\cdot3=14289،\\
476605\cdot5=2383025.
\end(array)" style="vertical-align: -125px; مرز: هیچ;">

و حالا توضیح وعده داده شده. الگوریتم بر اساس فرمول است