پای مخالف با پای مجاور. راست گوشه. نظریه تفصیلی با مثال

مثلثات شاخه ای از ریاضیات است که به مطالعه توابع مثلثاتی و همچنین کاربرد آنها در عمل می پردازد. این ویژگی ها عبارتند از سینوسی، کسینوس، مماس و کوتانژانت.

سینوس یک تابع مثلثاتی است، نسبت قدر پای مقابل به بزرگی هیپوتنوز.

سینوس در مثلثات

همانطور که در بالا ذکر شد، سینوس مستقیماً با مثلثات و توابع مثلثاتی مرتبط است. عملکرد آن توسط

کمک به محاسبه زاویه، مشروط بر اینکه ابعاد اضلاع مثلث مشخص باشد.
کمک به محاسبه اندازه ضلع مثلث، مشروط بر اینکه زاویه آن مشخص باشد.

باید به خاطر داشت که مقدار سینوس همیشه برای هر اندازه مثلث یکسان خواهد بود، زیرا سینوس یک اندازه گیری نیست، بلکه یک نسبت است.

در نتیجه، برای اینکه این مقدار ثابت برای هر راه حل یک مسئله خاص محاسبه نشود، جداول مثلثاتی خاصی ایجاد شد. در آنها مقادیر سینوس، کسینوس، مماس و کوتانژانت قبلا محاسبه و ثابت شده است. معمولاً این جداول بر روی برگه کتب درسی جبر و هندسه آورده شده است. آنها همچنین می توانند در اینترنت پیدا شوند.

سینوس در هندسه

هندسه نیاز به تجسم دارد، بنابراین، برای درک در عمل، سینوس یک زاویه چیست، باید یک مثلث با زاویه قائمه رسم کنید.

فرض کنید اضلاع تشکیل دهنده یک زاویه قائمه نامگذاری شده اند الف، ج،زاویه مخالف ایکس.

معمولا طول اضلاع در وظایف نشان داده شده است. بیایید بگوییم a=3، b=4. در این مورد، نسبت تصویر شبیه ¾ خواهد بود. علاوه بر این، اگر اضلاع مثلث مجاور زاویه حاد را طولانی کنیم ایکس، سپس طرفین افزایش می یابد آو که درو هیپوتنوس ضلع سوم مثلث قائم الزاویه است که با قاعده زاویه قائمه ندارد. اکنون اضلاع مثلث را می توان به طور متفاوت نامید، به عنوان مثال: m، n، k.

با این اصلاح، قانون مثلثات عمل کرد: طول اضلاع مثلث تغییر کرد، اما نسبت آنها تغییر نکرد.

دانشمندان باستان متوجه این واقعیت شدند که اگر طول اضلاع یک مثلث را هر چند بار که دوست دارید و با حفظ مقدار زاویه x تغییر دهید، نسبت بین اضلاع آن همچنان بدون تغییر باقی می ماند. در مورد ما، طول اضلاع می تواند به صورت زیر تغییر کند: a/b \u003d ¾، زمانی که پهلو بلند شد آتا 6 سانتی متر و که در- تا 8 سانتی متر بدست می آوریم: m/n = 6/8 = 3/4.

نسبت اضلاع در یک مثلث قائم الزاویه از این نظر را می گویند:

سینوس زاویه x نسبت پای مقابل به هیپوتانوس است: sinx = a/c.
کسینوس زاویه x نسبت پای مجاور به هیپوتانوس است: cosx = w/s;
مماس زاویه x نسبت پای مقابل به مجاور است: tgx \u003d a / b؛
کوتانژانت زاویه x نسبت پای مجاور به طرف مقابل است: ctgx \u003d در / a.

کدام یک از ما در مدرسه فریاد نمی زدیم که ریاضیات هرگز برای او مفید نخواهد بود. به نظر همه ما این بود که همه این فرمول های نامفهوم، معادلات دست و پا گیر و نام های پیچیده هیچ ربطی به زندگی واقعی ندارند. اما دیر یا زود، تمام دانشی که در مدرسه دریافت کردیم کاربرد خود را پیدا می کند. و دانستن اینکه سینوس، کسینوس یا مماس چیست می تواند شهرت شما را حفظ کند.

مقداری هندسه مدرسه

بنابراین، سینوس نسبت اضلاع در یک مثلث قائم الزاویه است. بیایید به یاد بیاوریم که یک مثلث قائم الزاویه از چه چیزی تشکیل شده است.

زاویه. مجموع زوایای یک مثلث 180 درجه است. زاویه قائمه 90 درجه است. این بدان معنی است که دو مورد باقی مانده نیز باید تا 90 درجه جمع شوند. یعنی یک زاویه قائمه داریم و دو زاویه حاد.

مهمانی. یک مثلث قائم الزاویه از یک هیپوتنوز و دو پایه تشکیل شده است. دو پا یک زاویه قائمه تشکیل می دهند و هیپوتنوس در مقابل آن قرار دارد.

سینوس یک زاویه چیست؟ همانطور که قبلا ذکر شد، این نسبت تصویر است. اما چی؟ سینوس یک زاویه حاد نسبت پای مقابل آن زاویه به هیپوتنوز است. بیایید به یک مثال نگاه کنیم:

سینوس زاویه A نسبت ضلع a (پای مقابل) به ضلع b (هیپوتنوز) خواهد بود.

سینوس زاویه C نسبت ضلع c (پایه مقابل ضلع C قرار دارد) به ضلع b (هیپوتنوز) خواهد بود.

یعنی اگر اضلاع a=3، c=4، b=5 باشند، سینوس زاویه A 5/3 و سینوس زاویه C 5/4 خواهد شد.

چه چیزی به ما می دهد؟ تا اینجا هیچی، اما بیایید به مثال دیگری نگاه کنیم. مثلث را با گسترش اضلاع بزرگ کنید. حالا ما این را داریم:

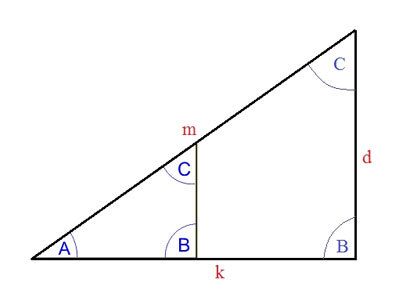
همانطور که از شکل مشخص است، طول اضلاع افزایش یافته است، اما زوایا نه. اما جالب تر از همه این است که نسبت ها نیز تغییر نکرده اند!

فرض کنید d=6، k=8، m=10. سپس سینوس زاویه A نسبت d/m = 6/10 خواهد بود. دو طرف معادله را کم می کنیم و همان 3/5 مورد اول را بدست می آوریم! و مهم نیست که چگونه اضلاع را تغییر دهید، بلند کنید یا کوتاه کنید، نسبت اضلاع همچنان یکسان خواهد بود.

بنابراین، واضح است که سینوس یک مقدار ثابت است.

و اکنون - مثلثات

یونانیان باستان مدتها پیش متوجه این موضوع شده بودند. سینوس های زوایای اصلی را محاسبه کردند و یادداشت کردند تا بتوانند همچنان از مقادیر آماده استفاده کنند و مقادیر جدیدی اختراع نکنند.

علاوه بر سینوس، زاویه دارای کسینوس (نسبت پای مجاور به هیپوتنوز)، مماس (نسبت پای مقابل به مجاور) و کوتانژانت (نسبت پای مجاور به همسایه) است. پای مخالف). همه این کمیت ها توابع مثلثاتی زاویه نامیده می شوند و برای محاسبات و حل مسئله استفاده می شوند.

میزهای مرموز برادیس

لازم نیست هر بار سینوس محاسبه شود. جداول Bradis مخصوصاً گردآوری شده است که در آنها همه سینوس ها، کسینوس ها، مماس ها و کوتانژانت ها قبلاً ثبت شده اند. از اینجا اطلاعات بدست می آوریم. مثلاً اگر زاویه ای را بشناسیم، سینوس و کسینوس آن را می شناسیم. یا برعکس - اگر سینوس یا کسینوس شناخته شده باشد - به راحتی می توانیم بفهمیم که کدام زاویه داده شده است.

طبیعتاً تعداد زیادی از این توابع مثلثاتی وجود دارد. به یاد آوردن همه آنها به سادگی غیرممکن است و در واقع ضروری نیست. اصولاً فقط برخی از آنها استفاده می شود.

کمی در مورد گوشه ها

اما نه تنها زوایای تند و راست دارای توابع مثلثاتی هستند، بلکه دارای توابع مبهم هستند، اما در اینجا یک دایره و یک نمودار از محورهای مختصات برای یافتن آنها از قبل مورد نیاز است. و این یک داستان کاملا متفاوت است.

سینوسی

حالا بیایید ببینیم سینوسی چیست. سینوسی شبیه به این است:

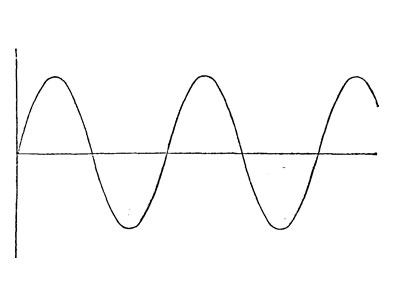
و نمودار تغییر سینوس بسته به تغییر زاویه است. همانطور که در بالا ذکر شد، طرفین می توانند تغییر کنند، و زاویه ثابت می ماند - سپس سینوس نیز بدون تغییر خواهد بود. اما اگر زاویه تغییر کند، نسبت ابعاد و در نتیجه مقدار سینوس تغییر می کند.

سینوسی تغییرات عددی سینوس یک زاویه را نشان می دهد و نمودار تابع y=sin(x) است. در اینجا هیچ چیز پیچیده ای وجود ندارد، به خصوص که مقادیر سینوس های تمام زوایا در جداول Bradis ثبت می شوند. اما ما فقط ابتدایی ترین آنها را به یاد خواهیم آورد.

کمی بیشتر در مورد تعیین زاویه

همه می دانند که زاویه ها بر حسب درجه یا رادیان اندازه گیری می شوند. درجه ها را با نقاله اندازه گیری می کنیم که شبیه یک نیم دایره است. یک درجه 1/360 دایره است. چرا دقیقا؟ زیرا هر گوشه ای می تواند "باز" یا "بسته" باشد. حتی می توانید آن را تا دور کامل باز کنید و یک دایره بگیرید.

همانطور که می دانید یک انقلاب کامل 360 o است. یک خط مستقیم زاویه 180 درجه است. یعنی قطر یک دایره 180 درجه است. یا عدد پی. بنابراین، معلوم می شود که زاویه می تواند 90 o (بر حسب درجه) یا Pi / 2 (بر حسب رادیان) باشد.

حالا بیایید سعی کنیم اساسی ترین سینوس ها را به خاطر بسپاریم. چه گوشه هایی بلافاصله به ذهن می رسد؟

زاویه راست - 90 o، Pi / 2 - sin \u003d 1

زاویه گسترش یافته - 180 o، Pi - sin \u003d 0

زاویه حاد 60 o - Pi / 3 - sin \u003d 0.866

زاویه حاد 45 o - Pi / 4 - sin \u003d 0.7071

سینوس، کسینوس، مماس، کتانژانت

مفاهیم سینوس ()، کسینوس ()، مماس ()، کوتانژانت () با مفهوم زاویه پیوند ناگسستنی دارند. برای درک خوب این مفاهیم پیچیده در نگاه اول (که باعث ایجاد حالت وحشت در بسیاری از دانش‌آموزان مدرسه می‌شود) و اطمینان یافتن از اینکه "شیطان به همان اندازه ترسناک نیست"، اجازه دهید از همان ابتدا شروع کنیم. و مفهوم زاویه را درک کنید.

مفهوم زاویه: رادیان، درجه

بیایید به تصویر نگاه کنیم. بردار نسبت به نقطه با مقدار مشخصی "چرخش" شد. بنابراین اندازه گیری این چرخش نسبت به موقعیت اولیه خواهد بود تزریق.

چه چیز دیگری در مورد مفهوم زاویه باید بدانید؟ خب، واحدهای زاویه، البته!

زاویه، هم در هندسه و هم در مثلثات، می تواند بر حسب درجه و رادیان اندازه گیری شود.

زاویه در (یک درجه) زاویه مرکزی در دایره است که بر اساس یک قوس دایره ای برابر با قسمت دایره است. بنابراین، کل دایره از "قطعات" کمان های دایره ای تشکیل شده است، یا زاویه توصیف شده توسط دایره برابر است.

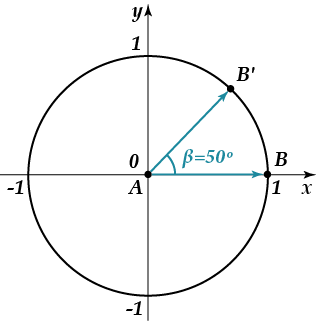
یعنی شکل بالا زاویه ای را نشان می دهد که مساوی است، یعنی این زاویه بر اساس یک قوس دایره ای به اندازه محیط است.

زاویه بر حسب رادیان را زاویه مرکزی در دایره می گویند که بر اساس یک کمان دایره ای است که طول آن برابر با شعاع دایره است. خوب فهمیدی؟ اگر نه، پس بیایید به تصویر نگاه کنیم.

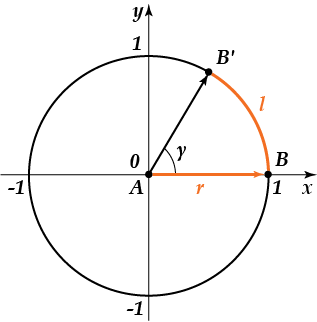
بنابراین، شکل زاویه ای برابر با رادیان را نشان می دهد، یعنی این زاویه بر اساس یک قوس دایره ای است که طول آن برابر با شعاع دایره است (طول برابر طول یا شعاع برابر است با طول قوس). بنابراین، طول قوس با فرمول محاسبه می شود:

زاویه مرکزی بر حسب رادیان کجاست.

خوب، با دانستن این موضوع، می توانید پاسخ دهید که چند رادیان دارای زاویه توصیف شده توسط یک دایره است؟ بله، برای این باید فرمول محیط دایره را به خاطر بسپارید. او اینجاست:

خوب، حالا بیایید این دو فرمول را به هم مرتبط کنیم و دریافت کنیم که زاویه توصیف شده توسط دایره برابر است. یعنی با همبستگی مقدار بر حسب درجه و رادیان، آن را دریافت می کنیم. به ترتیب، . همانطور که می بینید، بر خلاف "درجه"، کلمه "رادیان" حذف شده است، زیرا واحد اندازه گیری معمولاً از متن مشخص است.

رادیان چند است؟ خیلی خوب!

فهمیدم؟ سپس به جلو ببندید:

هیچ مشکلی؟ سپس نگاه کنید پاسخ می دهد:

مثلث قائم الزاویه: سینوس، کسینوس، مماس، کتانژانت یک زاویه

بنابراین، با مفهوم زاویه مشخص شد. اما سینوس، کسینوس، مماس، کتانژانت یک زاویه چیست؟ بیایید آن را بفهمیم. برای این کار، مثلث قائم الزاویه به ما کمک می کند.

اضلاع مثلث قائم الزاویه چه نام دارند؟ درست است، هیپوتنوز و پاها: هیپوتنوز سمتی است که در مقابل زاویه راست قرار دارد (در مثال ما، این طرف است). پاها دو ضلع باقیمانده و (آنهایی که مجاور زاویه قائم هستند) هستند، به علاوه، اگر پاها را نسبت به زاویه در نظر بگیریم، ساق پای مجاور، و پا در مقابل است. خب حالا بیایید به این سوال پاسخ دهیم: سینوس، کسینوس، مماس و کتانژانت یک زاویه چیست؟

سینوس یک زاویه- این نسبت پای مخالف (دور) به هیپوتنوز است.

در مثلث ما

کسینوس یک زاویه- این نسبت پای مجاور (نزدیک) به هیپوتنوز است.

در مثلث ما

مماس زاویه- این نسبت پای مخالف (دور) به مجاور (نزدیک) است.

در مثلث ما

کوتانژانت یک زاویه- این نسبت پای مجاور (نزدیک) به مخالف (دور) است.

در مثلث ما

این تعاریف لازم است یاد آوردن! برای اینکه راحت‌تر به خاطر بسپارید کدام پا را به چه چیزی تقسیم کنید، باید آن را به وضوح درک کنید مماسو کتانژانتفقط پاها می نشینند و هیپوتنوز فقط در داخل ظاهر می شود سینوسیو کسینوس. و سپس می توانید با زنجیره ای از انجمن ها بیایید. مثلا این یکی:

کسینوس← لمس← لمس← مجاور;

کوتانژانت← لمس← لمس← مجاور.

اول از همه، لازم به یادآوری است که سینوس، کسینوس، مماس و کوتانژانت به عنوان نسبت اضلاع یک مثلث به طول این ضلع ها (در یک زاویه) بستگی ندارد. باور نکن؟ سپس با دیدن عکس مطمئن شوید:

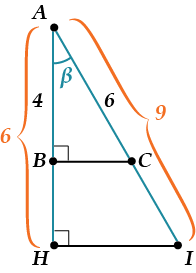
برای مثال کسینوس یک زاویه را در نظر بگیرید. طبق تعریف، از مثلث: ، اما ما می توانیم کسینوس یک زاویه را از مثلث محاسبه کنیم: . ببینید طول اضلاع متفاوت است، اما مقدار کسینوس یک زاویه یکسان است. بنابراین، مقادیر سینوس، کسینوس، مماس و کوتانژانت تنها به بزرگی زاویه بستگی دارد.

اگر تعاریف را فهمیدید، پس ادامه دهید و آنها را اصلاح کنید!

برای مثلثی که در شکل زیر نشان داده شده است، پیدا می کنیم.

خوب متوجه شدی؟ سپس خودتان آن را امتحان کنید: همان را برای گوشه محاسبه کنید.

دایره واحد (مثلثی).

با درک مفاهیم درجه و رادیان دایره ای با شعاع برابر در نظر گرفتیم. چنین دایره ای نامیده می شود تنها. در مطالعه مثلثات بسیار مفید است. بنابراین، ما کمی بیشتر در مورد آن صحبت می کنیم.

همانطور که می بینید، این دایره در سیستم مختصات دکارتی ساخته شده است. شعاع دایره برابر با یک است، در حالی که مرکز دایره در مبدا قرار دارد، موقعیت اولیه بردار شعاع در امتداد جهت مثبت محور ثابت است (در مثال ما، این شعاع است).

هر نقطه از دایره مربوط به دو عدد است: مختصات در امتداد محور و مختصات در امتداد محور. این اعداد مختصات چیست؟ و در کل چه ربطی به موضوع مورد بحث دارن؟ برای انجام این کار، مثلث قائم الزاویه در نظر گرفته شده را به خاطر بسپارید. در شکل بالا دو مثلث کامل قائم الزاویه را مشاهده می کنید. مثلثی را در نظر بگیرید. مستطیل شکل است زیرا بر محور عمود است.

از یک مثلث برابر با چه چیزی است؟ خیلی خوب. علاوه بر این، می دانیم که شعاع دایره واحد است، و بنابراین، . این مقدار را با فرمول کسینوس ما جایگزین کنید. در اینجا چیزی است که اتفاق می افتد:

و مساوی از مثلث چیست؟ خوب البته، ! مقدار شعاع را با این فرمول جایگزین کنید و بدست آورید:

بنابراین، می توانید به من بگویید مختصات یک نقطه که متعلق به دایره است چیست؟ خوب، هیچ راهی؟ و اگر متوجه شوید که فقط اعداد هستند؟ با چه مختصاتی مطابقت دارد؟ خوب، البته، مختصات! با چه مختصاتی مطابقت دارد؟ درست است، هماهنگ کنید! بنابراین، نکته.

و پس چه چیزی برابر است و؟ درست است، بیایید از تعاریف متناظر مماس و کوتانژانت استفاده کنیم و دریافت کنیم که، a.

اگر زاویه بزرگتر باشد چه؟ برای مثال، مانند این تصویر:

چه چیزی در این مثال تغییر کرده است؟ بیایید آن را بفهمیم. برای انجام این کار، دوباره به یک مثلث قائم الزاویه می رویم. مثلث قائم الزاویه را در نظر بگیرید: یک زاویه (به عنوان مجاور یک زاویه). مقدار سینوس، کسینوس، مماس و کوتانژانت یک زاویه چقدر است؟ درست است، ما به تعاریف مربوط به توابع مثلثاتی پایبند هستیم:

خوب، همانطور که می بینید، مقدار سینوس زاویه همچنان با مختصات مطابقت دارد. مقدار کسینوس زاویه - مختصات؛ و مقادیر مماس و کتانژانت به نسبت های مربوطه. بنابراین، این روابط برای هر چرخش بردار شعاع اعمال می شود.

قبلاً ذکر شد که موقعیت اولیه بردار شعاع در امتداد جهت مثبت محور است. تاکنون این بردار را در خلاف جهت عقربه های ساعت چرخانده ایم، اما اگر آن را در جهت عقربه های ساعت بچرخانیم چه اتفاقی می افتد؟ هیچ چیز خارق‌العاده‌ای نیست، شما همچنین زاویه‌ای با اندازه خاصی دریافت خواهید کرد، اما فقط منفی خواهد بود. بنابراین، هنگام چرخش بردار شعاع در خلاف جهت عقربه های ساعت، به دست می آوریم زوایای مثبتو هنگام چرخش در جهت عقربه های ساعت - منفی.

بنابراین، می دانیم که یک چرخش کامل از بردار شعاع در اطراف دایره یا است. آیا می توان بردار شعاع را با یا برحسب چرخش کرد؟ خوب، البته که می توانید! بنابراین، در حالت اول، بردار شعاع یک دور کامل می‌کند و در موقعیت یا توقف می‌کند.

در حالت دوم، یعنی بردار شعاع سه دور کامل می‌کند و در موقعیت یا توقف می‌کند.

بنابراین، از مثال‌های بالا، می‌توان نتیجه گرفت که زوایایی که با یا (جایی که هر عدد صحیحی است) متفاوت هستند، با موقعیت یکسان بردار شعاع مطابقت دارند.

شکل زیر یک زاویه را نشان می دهد. همان تصویر مربوط به گوشه و غیره است. این لیست را می توان به طور نامحدود ادامه داد. همه اینها را می توان با فرمول کلی یا (هر عدد صحیح کجاست) نوشت.

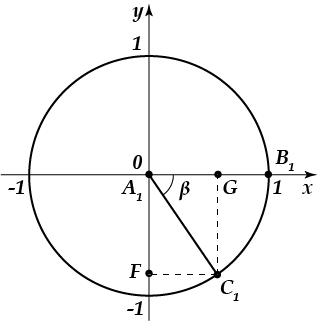
اکنون، با دانستن تعاریف توابع مثلثاتی اساسی و با استفاده از دایره واحد، سعی کنید پاسخ دهید که مقادیر برابر است:

در اینجا یک حلقه واحد برای کمک به شما وجود دارد:

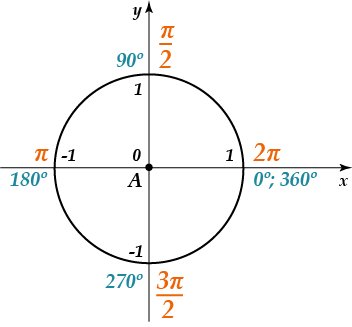
هیچ مشکلی؟ سپس بیایید آن را بفهمیم. پس می دانیم که:

از اینجا، مختصات نقاط مربوط به معیارهای زاویه خاص را تعیین می کنیم. خوب، بیایید به ترتیب شروع کنیم: گوشه در با یک نقطه با مختصات مطابقت دارد، بنابراین:

وجود ندارد؛

علاوه بر این، با رعایت همین منطق، متوجه می شویم که گوشه ها به ترتیب با نقاط دارای مختصات مطابقت دارند. با دانستن این موضوع، تعیین مقادیر توابع مثلثاتی در نقاط مربوطه آسان است. ابتدا خودتان آن را امتحان کنید، سپس پاسخ ها را بررسی کنید.

پاسخ ها:

وجود ندارد

بنابراین می توانیم جدول زیر را تهیه کنیم:

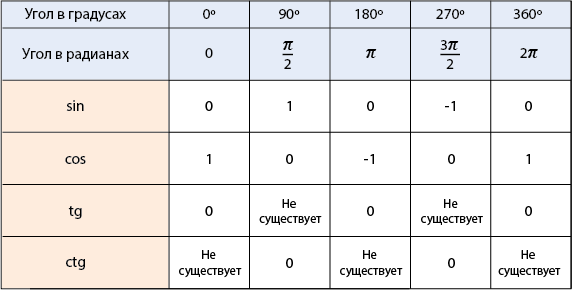
نیازی به یادآوری تمام این ارزش ها نیست. کافی است مطابقت بین مختصات نقاط روی دایره واحد و مقادیر توابع مثلثاتی را به خاطر بسپارید:

اما مقادیر توابع مثلثاتی زوایا در و داده شده در جدول زیر را باید به خاطر بسپارید:

نیازی به ترس نیست، اکنون یکی از نمونه هایی از حفظ نسبتاً ساده مقادیر مربوطه را نشان خواهیم داد:

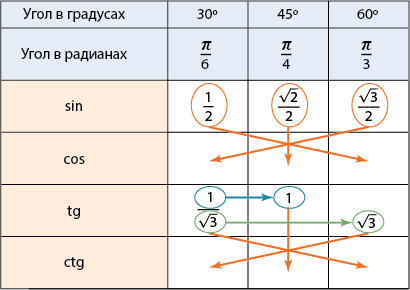
برای استفاده از این روش، به خاطر سپردن مقادیر سینوس برای هر سه معیار زاویه () و همچنین مقدار مماس زاویه c حیاتی است. با دانستن این مقادیر، بازیابی کل جدول بسیار آسان است - مقادیر کسینوس مطابق با فلش ها منتقل می شوند، یعنی:

با دانستن این موضوع، می توانید مقادیر مربوط به آن را بازیابی کنید. صورت " " مطابقت دارد و مخرج " " مطابقت دارد. مقادیر کوتانژانت مطابق با فلش های نشان داده شده در شکل منتقل می شوند. اگر این را فهمیدید و نمودار را با فلش به خاطر بسپارید، کافی است کل مقدار را از جدول به خاطر بسپارید.

مختصات یک نقطه روی یک دایره

آیا با دانستن مختصات مرکز دایره، شعاع و زاویه چرخش آن می توان نقطه ای (مختصات آن) را روی یک دایره پیدا کرد؟ خوب، البته که می توانید! بیایید یک فرمول کلی برای یافتن مختصات یک نقطه استخراج کنیم. در اینجا، برای مثال، ما چنین دایره ای داریم:

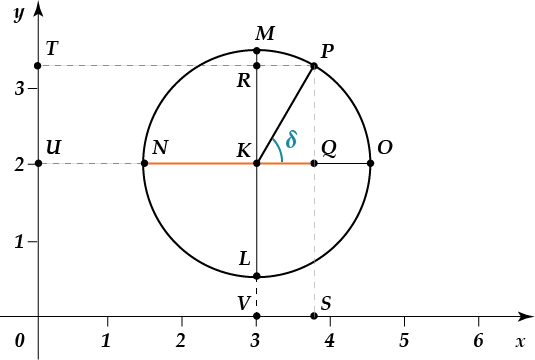
به ما داده می شود که نقطه مرکز دایره است. شعاع دایره برابر است. لازم است مختصات نقطه به دست آمده از چرخش نقطه به درجه را پیدا کنید.

همانطور که از شکل مشخص است، مختصات نقطه مطابق با طول قطعه است. طول قطعه مطابق با مختصات مرکز دایره است، یعنی برابر است با. طول یک قطعه را می توان با استفاده از تعریف کسینوس بیان کرد:

سپس ما آن را برای نقطه مختصات داریم.

با همین منطق، مقدار مختصات y را برای نقطه پیدا می کنیم. بدین ترتیب،

بنابراین، به طور کلی، مختصات نقاط با فرمول تعیین می شود:

مختصات مرکز دایره،

شعاع دایره،

زاویه چرخش بردار شعاع.

همانطور که می بینید، برای دایره واحدی که در نظر می گیریم، این فرمول ها به طور قابل توجهی کاهش می یابد، زیرا مختصات مرکز صفر است و شعاع برابر با یک است:

خوب، بیایید این فرمول ها را برای طعم دادن، تمرین یافتن نقاط روی یک دایره امتحان کنیم؟ پس تلاش کن:

1. مختصات یک نقطه را در یک دایره واحد که با روشن کردن یک نقطه به دست می آید، پیدا کنید.

2. مختصات یک نقطه را در یک دایره واحد که با چرخش یک نقطه روی آن به دست می آید، پیدا کنید.

3. مختصات یک نقطه را در یک دایره واحد که با روشن کردن یک نقطه به دست می آید، پیدا کنید.

4. نقطه - مرکز دایره. شعاع دایره برابر است. لازم است مختصات نقطه ای را که با چرخش بردار شعاع اولیه به دست می آید، پیدا کنیم.

5. نقطه - مرکز دایره. شعاع دایره برابر است. لازم است مختصات نقطه ای را که با چرخش بردار شعاع اولیه به دست می آید، پیدا کنیم.

هر گونه مشکل / سوال؟ سپس راه حل را پیدا کنید.

دیده می شود که. و ما می دانیم که چه چیزی مربوط به چرخش کامل نقطه شروع است. بنابراین، نقطه مورد نظر در همان موقعیتی قرار می گیرد که هنگام چرخش به. با دانستن این موضوع، مختصات مورد نظر نقطه را پیدا می کنیم:

2. دایره واحدی با مرکز در یک نقطه است، به این معنی که می توانیم از فرمول های ساده شده استفاده کنیم:

دیده می شود که. ما می دانیم که چه چیزی مربوط به دو چرخش کامل نقطه شروع است. بنابراین، نقطه مورد نظر در همان موقعیتی قرار می گیرد که هنگام چرخش به. با دانستن این موضوع، مختصات مورد نظر نقطه را پیدا می کنیم:

سینوس و کسینوس مقادیر جدولی هستند. ما ارزش های آنها را به خاطر می آوریم و دریافت می کنیم:

بنابراین نقطه مورد نظر دارای مختصاتی است.

3. دایره واحدی با مرکز در یک نقطه است، به این معنی که می توانیم از فرمول های ساده شده استفاده کنیم:

دیده می شود که. بیایید مثال در نظر گرفته شده را در شکل به تصویر بکشیم:

شعاع زاویه هایی با محور برابر با و می سازد. با دانستن اینکه مقادیر جدولی کسینوس و سینوس برابر هستند و با تعیین اینکه کسینوس در اینجا مقدار منفی می گیرد و سینوس مثبت است، داریم:

هنگام مطالعه فرمول های کاهش توابع مثلثاتی در مبحث، نمونه های مشابه با جزئیات بیشتری تحلیل می شوند.

بنابراین نقطه مورد نظر دارای مختصاتی است.

زاویه چرخش بردار شعاع (بر اساس شرایط)

برای تعیین علائم مربوط به سینوس و کسینوس، یک دایره و یک زاویه می سازیم:

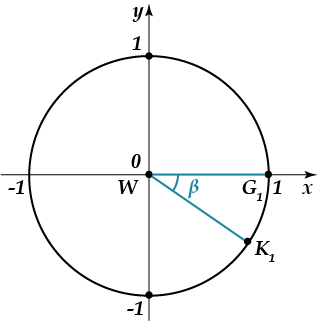
همانطور که می بینید، مقدار، یعنی مثبت است و مقدار، یعنی منفی. با دانستن مقادیر جدولی توابع مثلثاتی مربوطه، به دست می آوریم که:

بیایید مقادیر به دست آمده را در فرمول خود جایگزین کنیم و مختصات را پیدا کنیم:

بنابراین نقطه مورد نظر دارای مختصاتی است.

5. برای حل این مشکل از فرمول هایی به صورت کلی استفاده می کنیم که کجا

مختصات مرکز دایره (در مثال ما،

شعاع دایره (بر اساس شرایط)

زاویه چرخش بردار شعاع (بر اساس شرایط).

همه مقادیر را در فرمول جایگزین کنید و دریافت کنید:

و - مقادیر جدول. آنها را به خاطر می آوریم و در فرمول جایگزین می کنیم:

بنابراین نقطه مورد نظر دارای مختصاتی است.

در مشکلات، زاویه راست به هیچ وجه ضروری نیست - پایین سمت چپ، بنابراین باید یاد بگیرید که چگونه یک مثلث قائمه را به این شکل تشخیص دهید.

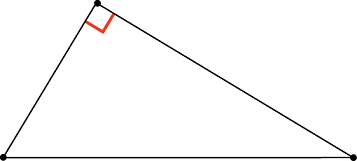
و در چنین

و در چنین

مثلث قائم الزاویه چیست؟ خب...اول اینکه اسم های زیبای خاصی برای مهمانی هاش هست.

به نقاشی توجه کنید!

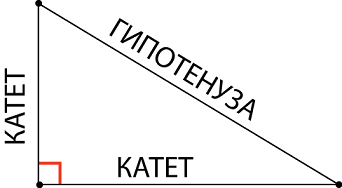
به یاد داشته باشید و اشتباه نگیرید: پاها - دو، و هیپوتنوز - فقط یک(تنها، منحصر به فرد و طولانی ترین)!

خوب، ما در مورد اسامی بحث کردیم، اکنون مهمترین چیز: قضیه فیثاغورث.

قضیه فیثاغورس.

این قضیه کلید حل بسیاری از مسائل مربوط به مثلث قائم الزاویه است. فیثاغورث در زمان های بسیار قدیم آن را ثابت کرد و از آن زمان فواید بسیاری برای کسانی که آن را می شناسند به ارمغان آورده است. و بهترین چیز در مورد آن این است که ساده است.

بنابراین، قضیه فیثاغورس:

این لطیفه را به خاطر دارید: "شلوار فیثاغورثی از همه طرف برابر است!"؟

اینها را بکشیم شلوار فیثاغورثیو به آنها نگاه کن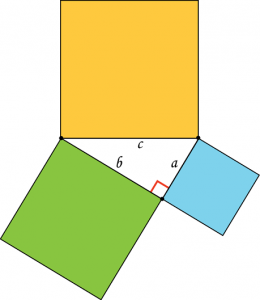

آیا واقعا شبیه شورت است؟ خوب، در کدام طرف و در کجا برابر هستند؟ این شوخی چرا و از کجا آمده است؟ و این لطیفه دقیقاً با قضیه فیثاغورث مرتبط است، دقیقاً با روشی که خود فیثاغورث قضیه خود را فرموله کرد. و آن را اینگونه بیان کرد:

"مجموع مساحت مربع ها، ساخته شده بر روی پاها، برابر است با مساحت مربعبر روی هیپوتنوز ساخته شده است.

کمی متفاوت به نظر نمی رسد، اینطور نیست؟ و بنابراین، هنگامی که فیثاغورث بیانیه قضیه خود را ترسیم کرد، دقیقاً چنین تصویری به دست آمد.

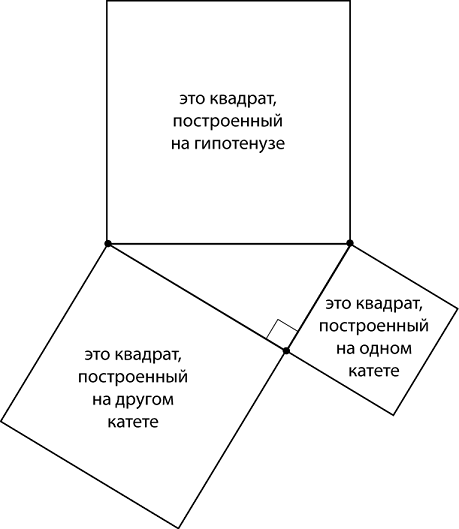
در این تصویر مجموع مساحت مربع های کوچک برابر با مساحت مربع بزرگ است. و برای اینکه بچه ها بهتر به یاد بیاورند که مجموع مربع های پاها برابر است با مربع هیپوتونوس ، شخصی شوخ طبع این شوخی را در مورد شلوار فیثاغورثی اختراع کرد.

چرا اکنون قضیه فیثاغورث را فرموله می کنیم؟

آیا فیثاغورث رنج کشید و در مورد مربع صحبت کرد؟

ببینید در زمان های قدیم ... جبر وجود نداشت! هیچ علامتی و غیره وجود نداشت. هیچ کتیبه ای وجود نداشت. آیا می توانید تصور کنید که چقدر برای دانش آموزان بیچاره باستانی وحشتناک بود که همه چیز را با کلمات حفظ کنند ؟؟! و ما می توانیم خوشحال باشیم که یک فرمول ساده از قضیه فیثاغورث داریم. بیایید دوباره آن را تکرار کنیم تا بهتر به خاطر بسپاریم:

حالا باید آسان باشد:

مربع هیپوتانوس برابر است با مجموع مربع های پاها.

خوب، مهم ترین قضیه در مورد مثلث قائم الزاویه مورد بحث قرار گرفت. اگر به چگونگی اثبات آن علاقه دارید، سطوح بعدی تئوری را بخوانید و اکنون به ادامه ... به جنگل تاریک ... مثلثات برویم! به کلمات وحشتناک سینوس، کسینوس، مماس و کوتانژانت.

سینوس، کسینوس، مماس، کتانژانت در مثلث قائم الزاویه.

در واقع، همه چیز اصلاً ترسناک نیست. البته تعریف واقعی سینوس، کسینوس، مماس و کوتانژانت را باید در مقاله بررسی کرد. اما شما واقعا نمی خواهید، نه؟ ما می توانیم خوشحال باشیم: برای حل مسائل مربوط به یک مثلث قائم الزاویه، به سادگی می توانید موارد ساده زیر را پر کنید:

چرا همه چیز در مورد گوشه است؟ گوشه کجاست؟ برای درک این موضوع، باید بدانید که عبارات 1 تا 4 چگونه در کلمات نوشته می شوند. نگاه کن، بفهم و به خاطر بسپار!

1.
در واقع اینگونه به نظر می رسد:

در مورد زاویه چطور؟ آیا پایی هست که مقابل گوشه یعنی پای مقابل (برای گوشه) باشد؟ البته دارند! این یک کاتت است!

اما در مورد زاویه چطور؟ از نزدیک نگاه کن. کدام پا در مجاورت گوشه است؟ البته گربه. این بدان معنی است که برای زاویه پا مجاور است، و

و اکنون، توجه! ببین چی بدست آوردیم:

ببینید چقدر عالیه:

حال به سراغ مماس و کتانژانت می رویم.

حالا چگونه آن را در قالب کلمات بیان کنیم؟ ساق نسبت به گوشه چیست؟ البته در مقابل - روبروی گوشه "نهفته است". و کتت؟ مجاور گوشه. پس چی به دست آوردیم؟

ببینید که چگونه صورت و مخرج معکوس می شوند؟

و حالا دوباره گوشه ها و مبادله انجام شد:

خلاصه

بیایید به اختصار آنچه را که آموخته ایم بنویسیم.

قضیه فیثاغورس:

این تبلت را به عنوان یک جدول ضرب به خاطر بسپارید - و می توانید بسیاری از مسائل مربوط به مثلث قائم الزاویه را حل کنید. در هر صورت، تمام وظایف قسمت اول امتحان که در آن یک مثلث قائم الزاویه درگیر است، قطعا برای شما “سخت” خواهد بود!
اگر می‌خواهید یاد بگیرید که چگونه مسائل پیچیده‌تر را حل کنید، باید حقایق شگفت‌انگیز بیشتری در مورد مثلث قائم‌الزاویه بیاموزید - سطوح تئوری زیر را بخوانید!

در ابتدا سینوس و کسینوس به دلیل نیاز به محاسبه کمیت ها در مثلث های قائم الزاویه به وجود آمدند. متوجه شدیم که اگر مقدار درجه اندازه گیری زوایای یک مثلث قائم الزاویه تغییر نکند، نسبت ابعاد، مهم نیست که این ضلع ها چقدر از نظر طول تغییر کنند، همیشه ثابت می ماند.

اینگونه بود که مفاهیم سینوس و کسینوس معرفی شدند. سینوس یک زاویه حاد در یک مثلث قائم الزاویه نسبت سمت مقابل به هیپوتنوز و کسینوس نسبت ساق مجاور به هیپوتنوز است.

قضایای کسینوس و سینوس

اما کسینوس و سینوس نه تنها در مثلث قائم الزاویه قابل استفاده هستند. برای یافتن مقدار زاویه منفرد یا تند، ضلع هر مثلث، کافی است قضیه کسینوس و سینوسی را اعمال کنیم.

قضیه کسینوس کاملاً ساده است: "مربع یک ضلع مثلث برابر است با مجموع مربع های دو ضلع دیگر منهای دو برابر حاصلضرب این ضلع ها به وسیله کسینوس زاویه بین آنها."

دو تفسیر از قضیه سینوس وجود دارد: کوچک و گسترده. به گزارش کوچک: «در مثلث، زاویه ها با اضلاع مقابل هم تناسب دارند». این قضیه اغلب به دلیل خاصیت دایره محصور در اطراف یک مثلث بسط می‌یابد: «در مثلث، زاویه‌ها با اضلاع مقابل هم تناسب دارند و نسبت آن‌ها برابر است با قطر دایره محصور شده».

مشتقات

مشتق یک ابزار ریاضی است که نشان می دهد یک تابع با توجه به تغییر در آرگومانش چقدر سریع تغییر می کند. مشتقات در جبر، هندسه، اقتصاد و فیزیک، تعدادی از رشته های فنی استفاده می شود.

هنگام حل مسائل، باید مقادیر جدولی مشتقات توابع مثلثاتی را بدانید: سینوس و کسینوس. مشتق سینوس کسینوس است و مشتق کسینوس سینوس است اما با علامت منفی.

کاربرد در ریاضیات

به خصوص اغلب از سینوس و کسینوس در حل مثلث قائم الزاویه و مسائل مربوط به آنها استفاده می شود.

راحتی سینوس ها و کسینوس ها نیز در فناوری منعکس شده است. ارزیابی زوایا و اضلاع با استفاده از قضایای کسینوس و سینوسی، شکستن اشکال و اجسام پیچیده به مثلث‌های "ساده" آسان بود. مهندسان و معماران که اغلب با محاسبات نسبت‌های ابعادی و اندازه‌گیری‌های درجه سر و کار دارند، زمان و تلاش زیادی را صرف محاسبه کسینوس و سینوس زوایای غیر جدولی کردند.

سپس جداول Bradis به کمک آمدند که حاوی هزاران مقدار سینوس، کسینوس، مماس و کوتانژانت از زوایای مختلف بود. در زمان شوروی، برخی از معلمان دانش آموزان خود را مجبور می کردند که صفحات جداول برادیس را حفظ کنند.

در یک مثلث قائم الزاویه، به عنوان ساده ترین چند ضلعی، دانشمندان مختلف دانش خود را در زمینه مثلثات در آن روزها تقویت کردند، زمانی که هیچ کس حتی این حوزه از ریاضیات را با آن کلمه نمی نامید. بنابراین، امروزه نمی توان به نویسنده ای اشاره کرد که در این شکل هندسی مسطح، الگوهایی را در نسبت طول اضلاع و بزرگی زوایا آشکار کرده است. چنین روابطی توابع مثلثاتی نامیده می شوند و به چندین گروه تقسیم می شوند که اصلی ترین آنها معمولاً توابع "مستقیم" در نظر گرفته می شوند. تنها دو تابع به این گروه اختصاص داده شده است که یکی از آنها سینوس است.

دستورالعمل

طبق تعریف، در مثلث قائم الزاویه یکی از زوایای آن برابر 90 درجه است و با توجه به اینکه مجموع زوایای آن در هندسه اقلیدسی باید برابر با 180 درجه باشد، دو زاویه دیگر تند هستند (یعنی کمتر از 90 درجه). ). قاعده مندی نسبت های دقیقاً این زوایا و طول ضلع ها توابع مثلثاتی را توصیف می کند.

تابعی که سینوس زاویه تند نامیده می شود، نسبت بین طول دو ضلع یک مثلث قائم الزاویه را تعیین می کند که یکی از آنها در مقابل این زاویه تند قرار دارد و دیگری در مجاورت آن و در مقابل زاویه قائمه قرار دارد. از آنجایی که ضلع مقابل زاویه قائمه در چنین مثلثی هیپوتنوز نامیده می شود و دو ضلع دیگر پاها هستند، تعریف تابع سینوس را می توان به عنوان نسبت بین طول های سمت مقابل و هیپوتنوز فرموله کرد.

علاوه بر چنین تعریف ساده ای از این تابع مثلثاتی، امروزه موارد پیچیده تری نیز وجود دارد: از طریق دایره در مختصات دکارتی، از طریق سری، از طریق حل معادلات دیفرانسیل و تابعی. این تابع پیوسته است، یعنی آرگومان های آن ("حوزه تعاریف") می تواند هر عددی باشد - از بی نهایت منفی تا بی نهایت مثبت. و حداکثر و حداقل مقادیر این تابع با محدوده -1 تا +1 محدود می شود - این "محدوده مقادیر آن" است. سینوس حداقل مقدار خود را در زاویه 270 درجه می گیرد که مربوط به 3/2 Pi است و حداکثر در 90 درجه (½ Pi) به دست می آید. مقادیر تابع در 0 درجه، 180 درجه، 360 درجه و غیره صفر می شود. از همه اینها نتیجه می شود که سینوس یک تابع تناوبی است و دوره آن برابر با 360 درجه یا دو برابر عدد Pi است.

برای محاسبات عملی مقادیر این تابع از یک آرگومان داده شده، می توانید از یک ماشین حساب استفاده کنید - اکثریت قریب به اتفاق آنها (از جمله ماشین حساب نرم افزاری داخلی سیستم عاملکامپیوتر شما) گزینه مربوطه را دارد.

ویدیو های مرتبط