چگونه بزرگترین قطر ذوزنقه را پیدا کنیم؟ مطالب مربوط به هندسه با موضوع "ذوزنقه و خواص آن"

قبل از اینکه بفهمیم چگونه قطر ذوزنقه را پیدا کنیم، بیایید به یاد بیاوریم که ذوزنقه چیست. در پلان سنجی، ذوزنقه چهار ضلعی است که دو ضلع مقابل آن با هم موازی هستند. این اضلاع موازی را قاعده ذوزنقه و بقیه را اضلاع می نامند. اضلاع می توانند یکسان باشند، پس با ذوزنقه متساوی الساقین روبرو هستیم.

در مرحله بعد، روش یافتن طول مورب ها را برای حالت کلی - یک ذوزنقه متساوی الساقین با جزئیات تجزیه و تحلیل خواهیم کرد. در این مورد، از این واقعیت پیش خواهیم رفت که داده های اولیه طول هر چهار طرف ذوزنقه است، زوایای پایه ناشناخته هستند.

محاسبه قطر ذوزنقه ای

ذوزنقه ABCD نشان داده شده در شکل دارای دو قطر AC و BD است. ترتیب یافتن طول آنها یکسان است، بنابراین بیایید همه چیز را با استفاده از مثال یافتن قطر BD مقابل ˂BAD در نظر بگیریم.

BD مورب نیز ضلعی از مثلث ABD است و با استفاده از قانون کسینوس با استفاده از فرمول قابل محاسبه است:

BD = √(AB 2 +AD 2 -2AB . AD . cos ˂BAD)

در این فرمول همه کمیت ها به جز کسینوس ˂BAD را می دانیم. برای محاسبه آن، باید تغییر کوچکی در تصویر انجام دهیم. مستطیل BNMC را از ذوزنقه اصلی "برش دهید". در نتیجه، مثلث ABD را بدست می آوریم، که در آن ضلع BD برابر با ضلع CD ذوزنقه ای خواهد بود.

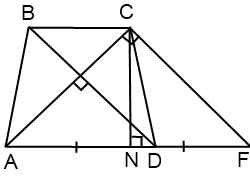
˂BAD" در مثلث برابر با ˂BAD در ذوزنقه است، زیرا ما هیچ تبدیلی با مثلث ABN انجام ندادیم. بنابراین، در این مثلث ABD" ضلع AB، ضلع BD" = CD و ضلع را می شناسیم. پس از میلاد" = پس از میلاد - NM = پس از میلاد - قبل از میلاد.

معلوم می شود که با قضیه کسینوس cos ˂BAD = cos ˂BAD" = (AB 2 + AD" 2 – BD" 2)/2AB . AD" = (AB 2 +(AD – BC) 2 – CD 2)/ 2AB. (میلادی-پیش از میلاد)

با جایگزین کردن عبارت به دست آمده با فرمول قبلی، دریافت می کنیم:

BD = √(AB 2 +AD 2 -2AB .AD .cos ˂BAD) = √(AB 2 +AD 2 -2AB .AD .(AB 2 +(AD - BC) 2 - CD 2)/2AB .(AD - BC)) \u003d √ (AB 2 + AD 2 - AD. (AB 2 + (AD - BC) 2 - CD 2) / (AD - BC)) \u003d √ (AB 2 + AD 2 - AD. ( بعد از میلاد - قبل از میلاد) 2 / (میلادی - قبل از میلاد) - پس از میلاد. (AB 2 - CD 2) / (میلادی - قبل از میلاد)) \u003d √ (AB 2 + AD 2 - AD 2 + AD. BC - AD. (AB 2 - CD 2 ) / (AD - BC)) \u003d √ (AB 2 + AD . BC - AD . (AB 2 - CD 2) / (AD - BC))

BD \u003d √ (AB 2 + AD . BC - AD . (AB 2 - CD 2) / (AD - BC))

فرمول حاصل برای قطر ذوزنقه برای هر مقدار طول اضلاع چهارضلعی اصلی معتبر است.

برای قطر دوم، فرمول بر این اساس شکل زیر را دارد:

AC \u003d √ (CD 2 + AD . BC - AD . (CD 2 - AB 2) / (AD - BC))

قطر ذوزنقه متساوی الساقین

اگر به نحوه یافتن قطر ذوزنقه متساوی الساقین علاقه مند هستید، فرمول حاصل را می توان تا حد زیادی ساده کرد. در واقع ، در ذوزنقه متساوی الساقین AB \u003d CD ، بنابراین AB 2 - CD 2 \u003d 0 و فرمول طول مورب به شکل کاهش می یابد:

BD = √(AB 2 + AD . BC)

قطرهای یک ذوزنقه متساوی الساقین با یکدیگر برابرند، بنابراین قطر دوم با همان فرمول پیدا می شود.

در صورتی که داده های اولیه طول قاعده ذوزنقه، یکی از اضلاع و زوایای قاعده باشد، پس کار یافتن قطر ذوزنقه به محاسبه ضلع مثلث با استفاده از قضیه کسینوس کاهش می یابد. .

بنابراین، ما یکی از آنها را صدا خواهیم کرد بزرگ ، دومین - پایه کوچک ذوزنقه ای ارتفاع ذوزنقه را می توان هر بخش از یک عمود کشیده شده از رئوس به سمت مقابل مربوطه نامید (برای هر راس دو ضلع مخالف وجود دارد) که بین راس گرفته شده و طرف مقابل محصور شده است. اما می توان "نوع خاصی" از ارتفاعات را مشخص کرد.
تعریف 8. ارتفاع قاعده ذوزنقه قسمتی از یک خط مستقیم عمود بر پایه ها است که بین پایه ها محصور شده است.
قضیه 7 . خط وسط ذوزنقه موازی قاعده ها و برابر با نصف مجموع آنهاست.
اثبات اجازه دهید ذوزنقه ABCD و خط وسط KM داده شود. بین نقاط B و M خط بکشید. سمت AD را تا نقطه D ادامه می دهیم تا با BM قطع شود. مثلث های BCm و MPD در ضلع و دو زاویه برابر هستند (CM=MD، ∠ BCM=∠ MDP - همپوشانی، ∠ BMC=∠ DMP - عمودی)، بنابراین VM=MP یا نقطه M نقطه وسط BP است. KM خط وسط در مثلث ABP است. با توجه به ویژگی خط وسط مثلث، KM موازی با AP و به ویژه AD است و برابر با نصف AP است:

قضیه 8 . مورب ها ذوزنقه را به چهار قسمت تقسیم می کنند که دو قسمت آن مجاور اضلاع برابر است.
یادآوری می کنم که ارقام اگر مساحت یکسانی داشته باشند برابر نامیده می شوند. مثلث های ABD و ACD مساحت و مساحت دارند ارتفاعات مساوی(با رنگ زرد مشخص شده است) و یک پایه مشترک. این مثلث ها هستند بخش کلی AOD. محدوده آنها را می توان به شرح زیر گسترش داد: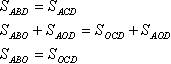

انواع ذوزنقه:
تعریف 9. (شکل 1) ذوزنقه حاد زاویه ای ذوزنقه ای است که در آن زوایای مجاور قاعده بزرگتر حاد است.
تعریف 10. (شکل 2) ذوزنقه منفرد ذوزنقه ای است که در آن یکی از زوایای مجاور قاعده بزرگتر منفرد است.
تعریف 11. (شکل 4) ذوزنقه ای را مستطیل می گویند که یک ضلع آن بر پایه ها عمود باشد.
تعریف 12. (شکل 3) متساوی الساقین (تساوی الساقین، متساوی الساقین) ذوزنقه ای است که اضلاع آن برابر است.

خواص ذوزنقه متساوی الساقین:
قضیه 10 . زوایای مجاور هر یک از قاعده های یک ذوزنقه متساوی الساقین برابر است.
اثبات برای مثال، تساوی زوایای A و D را با پایه بزرگتر AD یک ذوزنقه متساوی الساقین ABCD ثابت کنیم. برای این منظور از نقطه C به موازات ضلع جانبی AB یک خط مستقیم می کشیم. پایه بزرگ را در نقطه M قطع خواهد کرد. ABCM چهار ضلعی متوازی الاضلاع است، زیرا از نظر ساخت دارای دو جفت ضلع موازی است. بنابراین، قطعه CM خط برش محصور در داخل ذوزنقه برابر است با ضلع جانبی آن: CM=AB. از اینجا مشخص می شود که CM=CD، مثلث CMD متساوی الساقین، ∠CMD=∠CDM و بنابراین، ∠A=∠D است.زوایای مجاور قاعده کوچکتر نیز مساوی هستند، زیرا برای آنهایی هستند که یک طرفه داخلی یافت می شوند و دارای مجموع دو خط هستند.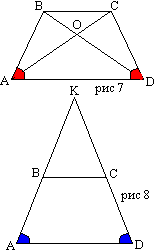
قضیه 11 . قطرهای ذوزنقه متساوی الساقین برابر است.
اثبات مثلث های ABD و ACD را در نظر بگیرید. در دو ضلع و زاویه بین آنها برابر است (AB=CD، AD مشترک است، زوایای A و D مطابق قضیه 10 برابر هستند). بنابراین AC=BD.

قضیه 13 . مورب های یک ذوزنقه متساوی الساقین با نقطه تقاطع به بخش های مشابه تقسیم می شوند. مثلث های ABD و ACD را در نظر بگیرید. در دو ضلع و زاویه بین آنها برابر است (AB=CD، AD مشترک است، زوایای A و D مطابق قضیه 10 برابر هستند). بنابراین، ∠ ОАD=∠ ОDA، از این رو زوایای ОВС و OSV برابر با زوایای همپوشانی ODA و OAD هستند. این قضیه را به یاد بیاورید: اگر دو زاویه در یک مثلث مساوی باشند، آنگاه متساوی الساقین است، بنابراین مثلث های ОВС و ОAD متساوی الساقین هستند که به معنای OS=OB و OA=OD و غیره است.
ذوزنقه متساوی الساقین یک شکل متقارن است.
تعریف 13. محور تقارن ذوزنقه متساوی الساقین به خط مستقیمی گفته می شود که از وسط قاعده های آن می گذرد.
قضیه 14 . محور تقارن ذوزنقه متساوی الساقین بر قاعده های آن عمود است.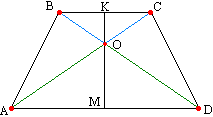
در قضیه 9 ثابت کردیم که خطی که به نقاط میانی پایه های ذوزنقه می پیوندد از نقطه تلاقی قطرها می گذرد. بعد (قضیه 13) ثابت کردیم که مثلث های AOD و BOC متساوی الساقین هستند. OM و OK به ترتیب وسط این مثلث ها طبق تعریف هستند. ویژگی مثلث متساوی الساقین را به یاد بیاورید: میانه یک مثلث متساوی الساقین که تا قاعده پایین آمده است، ارتفاع مثلث نیز می باشد. با توجه به عمود بودن پایه های قسمت های خط مستقیم KM، محور تقارن بر پایه ها عمود است.
علائمی که ذوزنقه متساوی الساقین را در بین همه ذوزنقه ها متمایز می کند:
قضیه 15 . اگر زوایای مجاور یکی از پایه های ذوزنقه مساوی باشد، ذوزنقه متساوی الساقین است.
قضیه 16 . اگر قطرهای ذوزنقه مساوی باشد، ذوزنقه متساوی الساقین است.
قضیه 17 . اگر اضلاع جانبی ذوزنقه که تا محل تقاطع امتداد یافته است، همراه با قاعده بزرگ آن یک مثلث متساوی الساقین تشکیل دهند، آنگاه ذوزنقه متساوی الساقین است.
قضیه 18 . اگر بتوان یک ذوزنقه را به صورت دایره ای حک کرد، آنگاه متساوی الساقین است.
علامت ذوزنقه مستطیل شکل:
قضیه 19 . هر چهار ضلعی که فقط دو زاویه قائمه در رئوس مجاور داشته باشد ذوزنقه مستطیلی(بدیهی است که دو ضلع موازی هستند، زیرا ضلع های یک طرفه برابر هستند. در صورتی که سه زاویه قائمه مستطیل باشند)
قضیه 20 . شعاع دایره حک شده در ذوزنقه برابر با نصف ارتفاع قاعده است.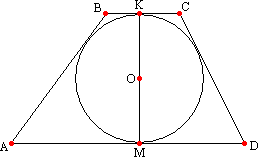
اثبات این قضیه توضیح این است که شعاع های کشیده شده به قاعده ها در ارتفاع ذوزنقه قرار دارند. از نقطه O - مرکز دایره ABCD که در این ذوزنقه حک شده است، شعاع ها را به نقاط تماس با پایه های آن ذوزنقه می کشیم. همانطور که می دانید، شعاع رسم شده به نقطه تماس عمود بر مماس است، بنابراین OK ^ BC و OM ^ AD. این قضیه را به خاطر بیاورید: اگر خطی بر یکی از خطوط موازی عمود باشد، بر خط دوم نیز عمود است. از این رو، خط OK نیز عمود بر AD است. بنابراین، دو خط عمود بر خط AD از نقطه O عبور می کنند که نمی تواند باشد، بنابراین این خطوط بر هم منطبق می شوند و عمود مشترک KM را تشکیل می دهند که برابر است با مجموع دو شعاع و قطر دایره محاط است. r=KM/2 یا r=h/2.
قضیه 21 . مساحت ذوزنقه برابر است با حاصل ضرب نصف مجموع پایه ها و ارتفاع پایه ها.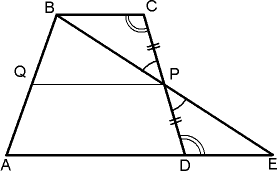

اثبات:بگذارید ABCD ذوزنقه ای باشد و AB و CD پایه های آن باشند. همچنین فرض کنید AH ارتفاع کاهش یافته از نقطه A به خط CD باشد. سپس S ABCD = S ACD + S ABC .
اما S ACD = 1/2AH CD و S ABC = 1/2AH AB.
بنابراین، S ABCD = 1/2AH (AB + CD).
Q.E.D.

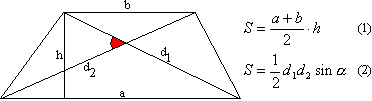فرمول دوم از چهارضلعی حرکت کرده است.

آشنایی با ذوزنقه برای اولین بار هنگام مطالعه دوره پلان سنجی اتفاق می افتد. اگرچه پیش از آن احتمالاً اشیایی را ملاقات کرده اید که شکل آنها با این شکل هندسی مطابقت دارد. یک چهار ضلعی از این نظر متفاوت است که از چهار ضلع آن فقط دو ضلع موازی هستند. اگر رئوس مقابل شکل را با پاره ها وصل کنیم، قطرهای آن را به دست می آوریم. چگونه طول آنها را تعیین کنیم؟ اندازه این قطعات به زوایای شکل، طول اضلاع و ارتفاع آن مربوط می شود.

مورب ها و زوایای ذوزنقه

اگر ذوزنقه دلخواه با زوایای شناخته شدهدر پایه، و همچنین اضلاع و پایه، سپس نسبت زیر به تعیین اندازه قطرها کمک می کند:

d1 \u003d √a 2 + d 2 - 2ad * cosβ،
d2 \u003d √a 2 + c 2 - 2ac * cosα،

d1، d2 قطرهای مورد نیاز هستند،
تحقیر نمودن،
ج، د - طرفین،
β، α زوایایی هستند که در قاعده قرار دارند.

این بر اساس قضیه کسینوس است که به شما امکان می دهد طول یک ضلع در یک مثلث را با استفاده از مقادیر شناخته شده دو ضلع دیگر و همچنین زاویه ای که در مقابل ضلع مورد نظر قرار دارد تعیین کنید.

مورب ها و اضلاع ذوزنقه

• اگر هر چهار ضلع شکل مشخص باشد، برای یافتن قطرهای آن، می توانید از عبارت زیر استفاده کنید:

d1 \u003d √ d 2 + ab - (a (d 2 - c 2) / (a-b))،
d2 \u003d √ c 2 + ab - (a (c 2 - d 2) / (a-b)).

• رابطه بین قطرها:

d1 2 + d2 2 = c 2 + d 2 + 2ab،
d1 \u003d √c 2 + d 2 + 2ab - d2 2،
d2 \u003d √c 2 + d 2 + 2ab - d1 2،

در هر دو مورد اول و دوم:
d1، d2 قطرهای مورد نیاز هستند،
a، b - پایه ها،
ج، د - طرف های جانبی.

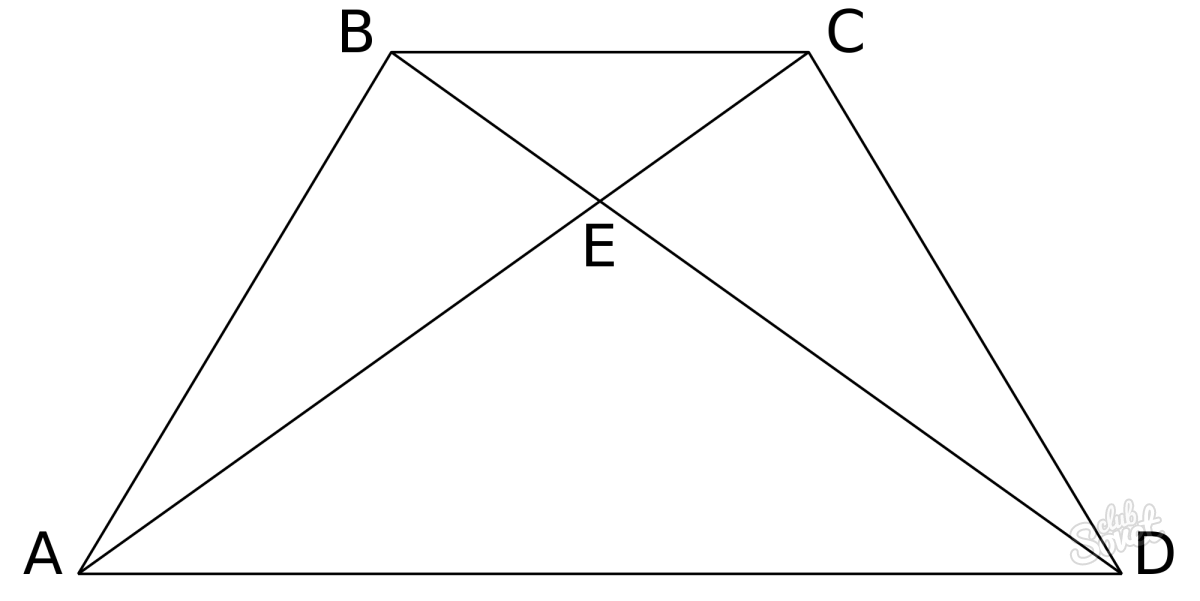
قطرها و ارتفاع ذوزنقه

در ارزش شناخته شدهیکی از پایه های شکل یا ضلع، زاویه در پایه پایین و همچنین ارتفاع چهارضلعی، تعیین طول قطرها نیز دشوار نخواهد بود.

اگر طبق شرایط انتساب، ذوزنقه اضلاع مساوی داشته باشد، عبارات برای یافتن قطرهای شکل با در نظر گرفتن این واقعیت تبدیل می شوند که c=d:

d1 = d2 = √c2 + ab،
d1 \u003d d2 \u003d √a 2 + c 2 - 2ac * cosα،
d1 = d2 = √a 2 + c 2 + 2ac*cosβ،
d1 \u003d d2 \u003d √b 2 + c 2 - 2bc * cosβ،
d1 = d2 = √b 2 + c 2 + 2bc*cosα،
d1 = d2 = √h 2 + l 2،
d1 = d2 = √h 2 + (a + b) 2/4،
d1 = d2 = √h*(a+b)/sinφ = √2S/ sinφ = √2lh/sinφ (sinφ = sin γ)،

d1، d2 قطرهای مورد نیاز هستند،
φ، γ زوایای بین آنها هستند،
h ارتفاع شکل است،
S - منطقه،
a، b پایه هستند (a< b),
ج - سمت،
l خط وسط است.

اگر قطرهای یک ذوزنقه متساوی الساقین عمود بر هم باشند، مطالب نظری زیر برای حل مسئله مفید خواهد بود.

1. اگر قطرها در ذوزنقه متساوی الساقین عمود باشند، ارتفاع ذوزنقه نصف مجموع قاعده هاست.

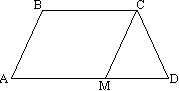
اجازه دهید خط CF را از طریق نقطه C به موازات BD رسم کنیم و خط AD را تا زمانی که CF را قطع کند گسترش دهیم.

چهار ضلعی BCFD متوازی الاضلاع است (BC∥ DF به عنوان پایه ذوزنقه، BD∥ CF توسط ساخت). بنابراین CF=BD، DF=BC و AF=AD+BC.

مثلث ACF قائم الزاویه است (اگر خطی عمود بر یکی از دو خط موازی باشد، بر خط دیگر نیز عمود است). از آنجایی که قطرهای یک ذوزنقه متساوی الساقین برابر هستند و CF=BD، پس CF=AC، یعنی مثلث ACF متساوی الساقین با قاعده AF است. از این رو، ارتفاع آن CN نیز میانه است. و از آنجایی که میانه راست گوشهکشیده شده به هیپوتانوس برابر با نیمی از آن است، پس

که می توان آن را به صورت کلی نوشت

جایی که h ارتفاع ذوزنقه است، a و b پایه های آن هستند.

2. اگر در ذوزنقه متساوی الساقین مورب ها عمود باشند، ارتفاع آن برابر با خط وسط است.

از آنجایی که خط وسط ذوزنقه m برابر است با نصف مجموع قاعده ها، پس

3. اگر قطرها در ذوزنقه متساوی الساقین عمود باشند، مساحت ذوزنقه برابر است با مربع ارتفاع ذوزنقه (یا مربع نیمی از مجموع قاعده ها یا مربع خط وسط). ).

از آنجایی که مساحت ذوزنقه با فرمول پیدا می شود

و ارتفاع، نصف مجموع قاعده ها و خط وسط یک ذوزنقه متساوی الساقین با قطرهای عمود بر هم برابر است:

G.I. کووالوا

روش بررسی خواص ذوزنقه

در مواد آزمون ها و امتحانات مختلف، اغلب وظایف ذوزنقه ای یافت می شود که حل آنها مستلزم دانستن ویژگی های "غیر برنامه ای" ذوزنقه است. (خواص خط وسط ذوزنقه، خواص مورب و زوایای ذوزنقه متساوی الساقین را نرم افزار می دانند.) خواص قابل توجه ذوزنقه چیست؟ کجا و چه زمانی آنها را در یک دوره هندسه مدرسه مطالعه کنیم؟

پس از مطالعه خواص خط وسط ذوزنقه می توان فرموله و اثبات کرد ویژگی قطعه ای که نقاط میانی قطرهای ذوزنقه را به هم متصل می کند. پاره ای که نقاط میانی قطرهای ذوزنقه را به هم وصل می کند با نصف اختلاف پایه ها برابر است.

با تمرین تکنیک اصلی برای حل مسائل روی ذوزنقه "دو ارتفاع را بکشید" ، دانش آموزان باید این کار را ارائه دهند: "اجازه دهید BTارتفاع ذوزنقه متساوی الساقین است آ ب پ تبا دلایل قبل از میلاد مسیحو آگهی.

,

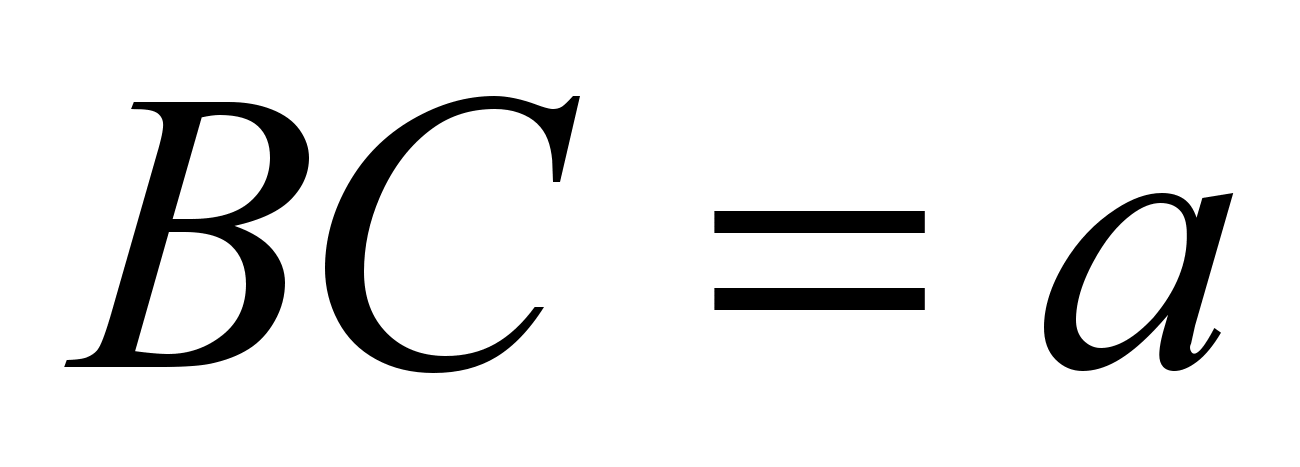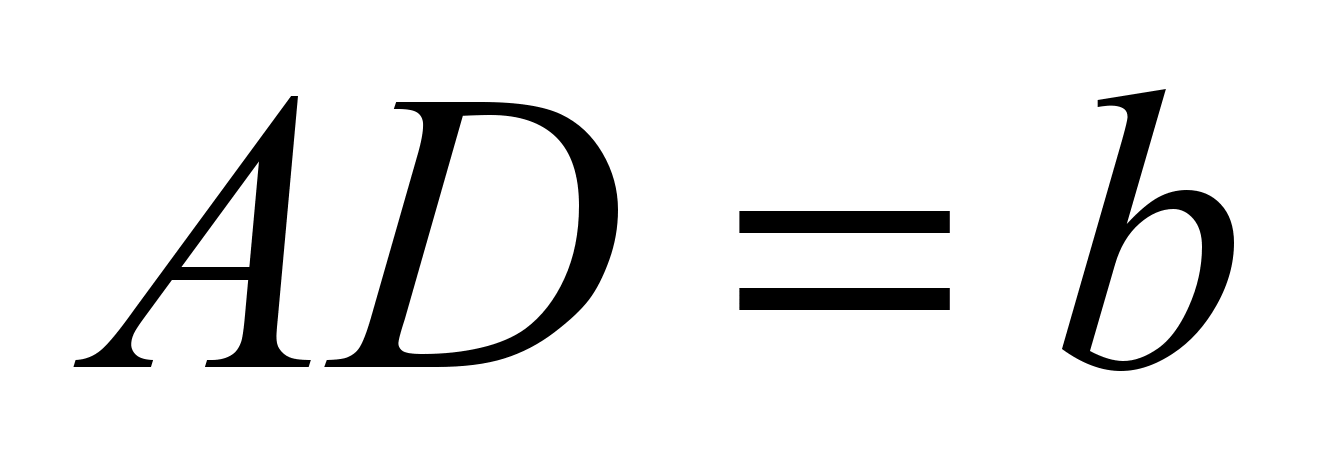. طول قطعات را پیدا کنید ATو TD».

مبحث "شبیه شکل ها" برای مطالعه خواص ذوزنقه بسیار مفید است. به عنوان مثال، قطرهای ذوزنقه آن را به چهار مثلث تقسیم می کنند و مثلث های مجاور پایه ها مشابه و مثلث های مجاور اضلاع برابر هستند. بیایید این بیانیه را بنامیم باخاصیت مثلث هایی که ذوزنقه بر اساس قطرهایش به آنها تقسیم می شود. علاوه بر این، بخش اول این ادعا به راحتی از طریق علامت شباهت مثلث ها در دو زاویه ثابت می شود. قسمت دوم را می توان در قالب تکلیف به دانش آموزان ارائه داد.

به همین ترتیب، مثلث ها BOCو AOBاگر پايه ها را پايه ها در نظر بگيريم، ارتفاع مشتركي دارند COو OA. سپس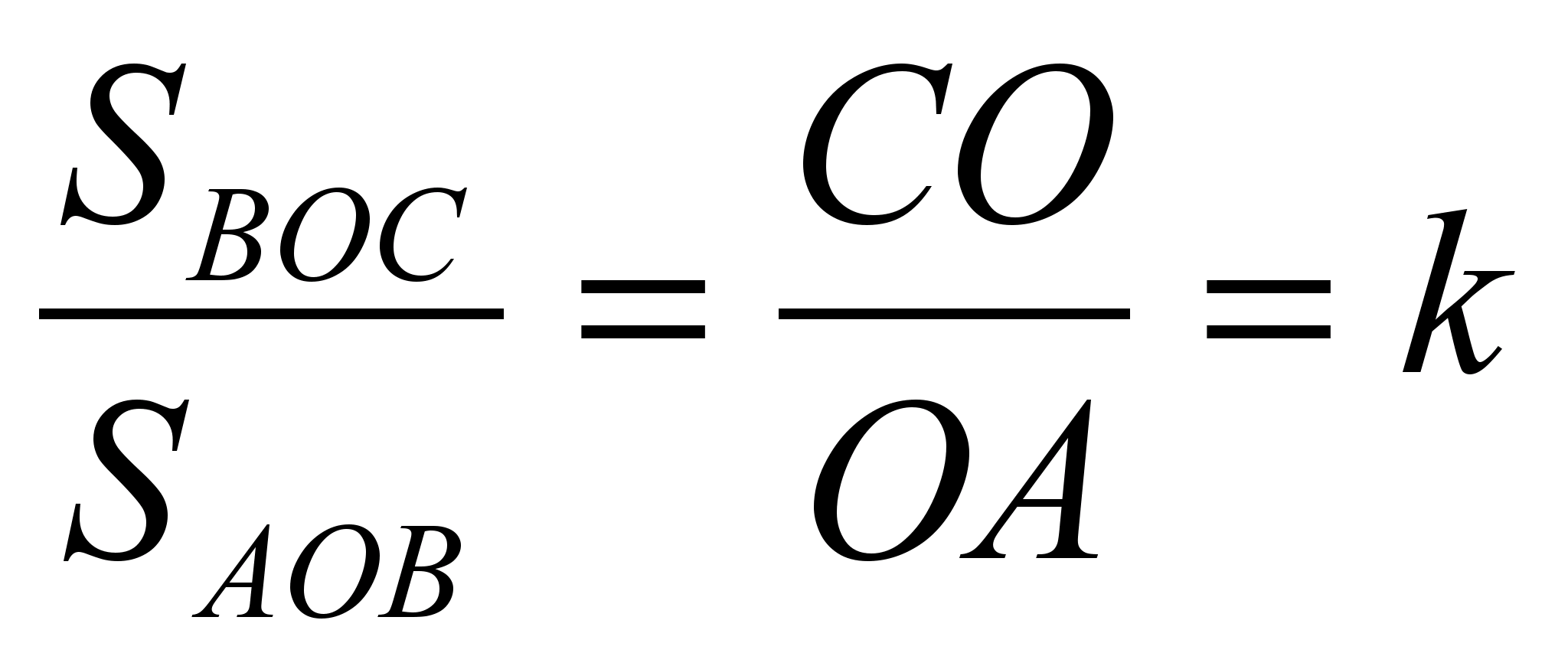

و

.

از این دو گزاره بر می آید که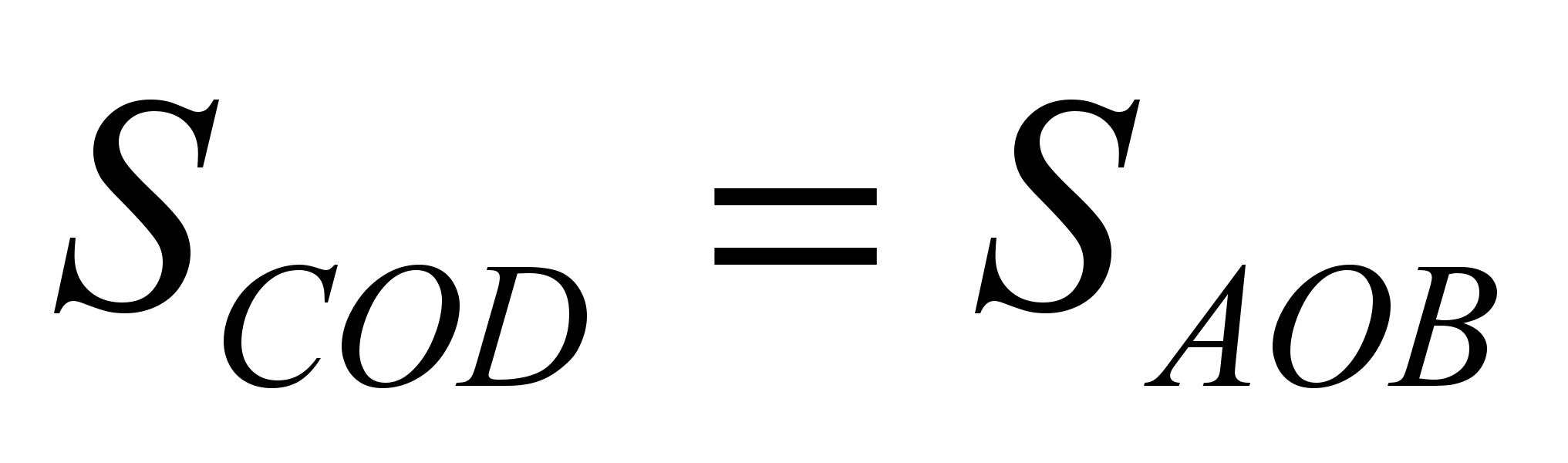

.

خیلی خوب است که روی بیانیه فرموله شده تمرکز نکنیم، بلکه پیدا کنیم رابطه بین مساحت های مثلثی که ذوزنقه با قطرهایش به آنها تقسیم می شود ، از دانش آموزان دعوت می کند تا مشکل را حل کنند: O نقطه تقاطع قطرهای ذوزنقه باشد. آ ب پ تبا دلایل قبل از میلاد مسیحو آگهی. معلوم است که مساحت مثلث ها BOCو AODبه ترتیب برابر 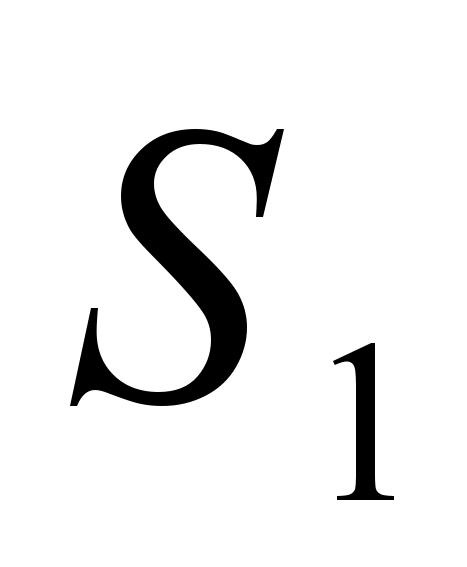و . مساحت ذوزنقه را پیدا کنید.

زیرا . از این رو، از شباهت مثلث ها بOسیو AODبه دنبال آن است

.در نتیجه،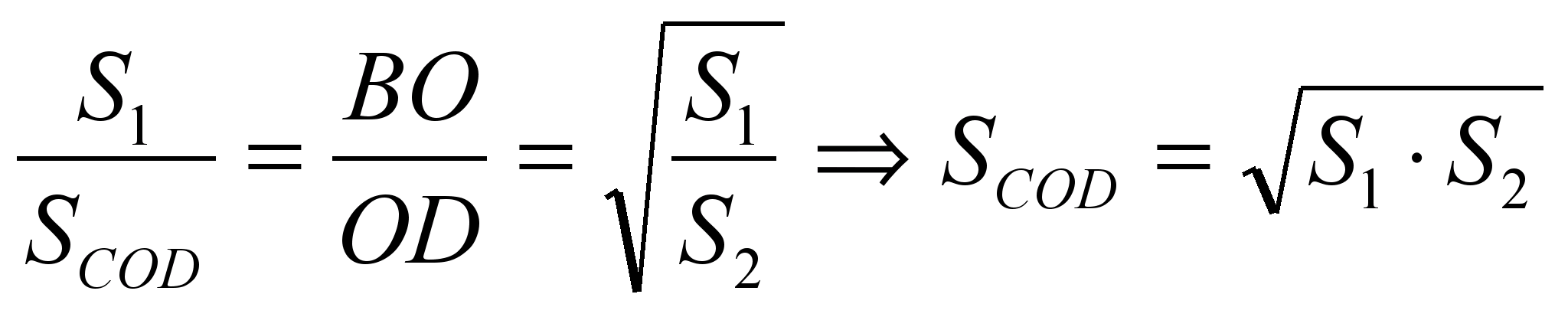

. سپس

با استفاده از شباهت نیز می توان اثبات کرد خاصیت قطعه ای که از نقطه تقاطع قطرهای ذوزنقه موازی با پایه ها عبور می کند. از دانش آموزان دعوت می کنیم تا این مسئله را حل کنند: "بگذارید O نقطه تقاطع قطرهای ذوزنقه باشد. آ ب پ تبا دلایل قبل از میلاد مسیحو آگهی. ، . طول قطعه را پیدا کنید PKعبور از نقطه تلاقی قطرهای ذوزنقه به موازات پایه ها. به چه بخش هایی تقسیم می شود؟ PKنقطه O».

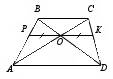
از اینجا

.

به همین ترتیب، از تشابه مثلث ها D.O.K.و DBC، به دنبال آن است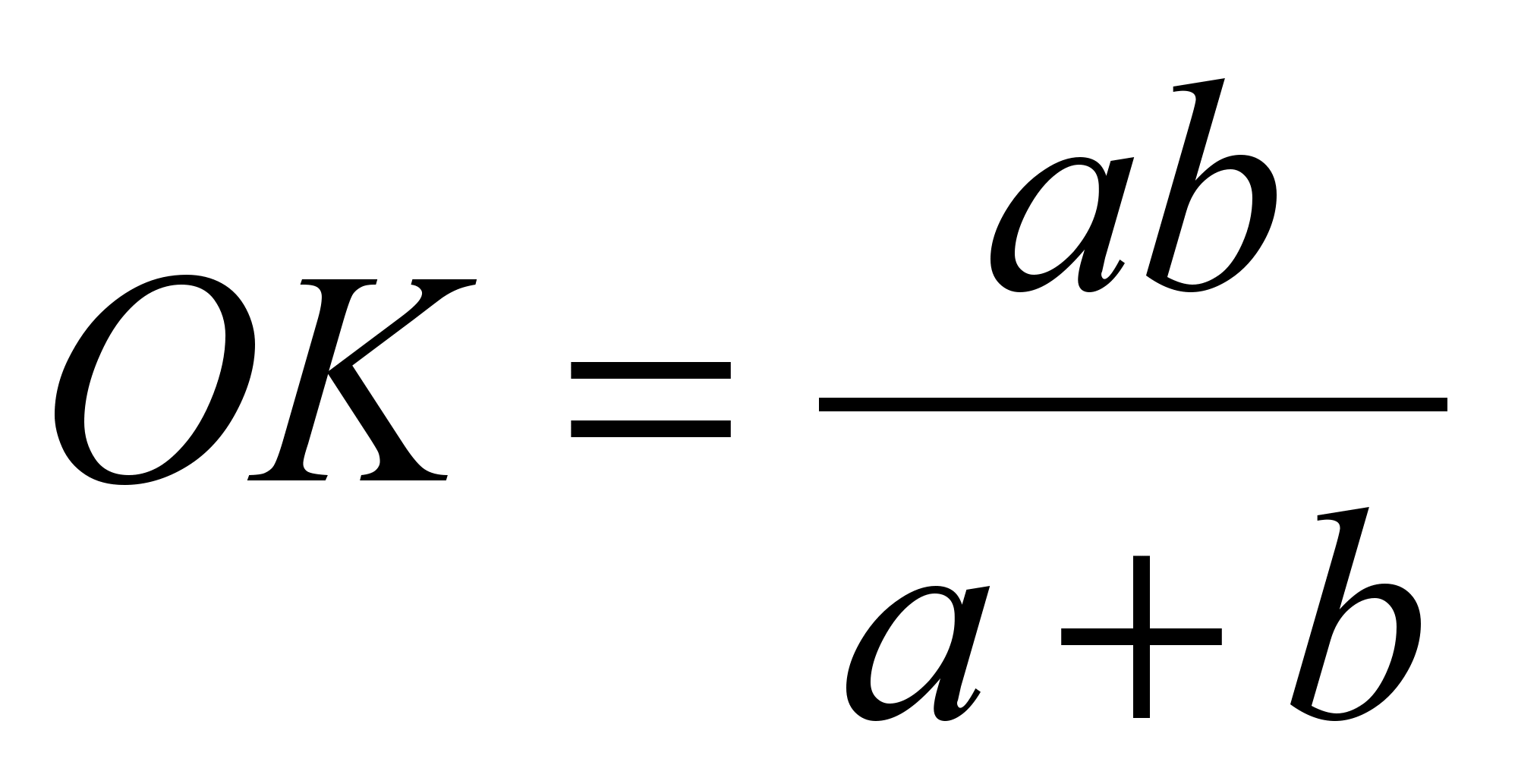

. از اینجا

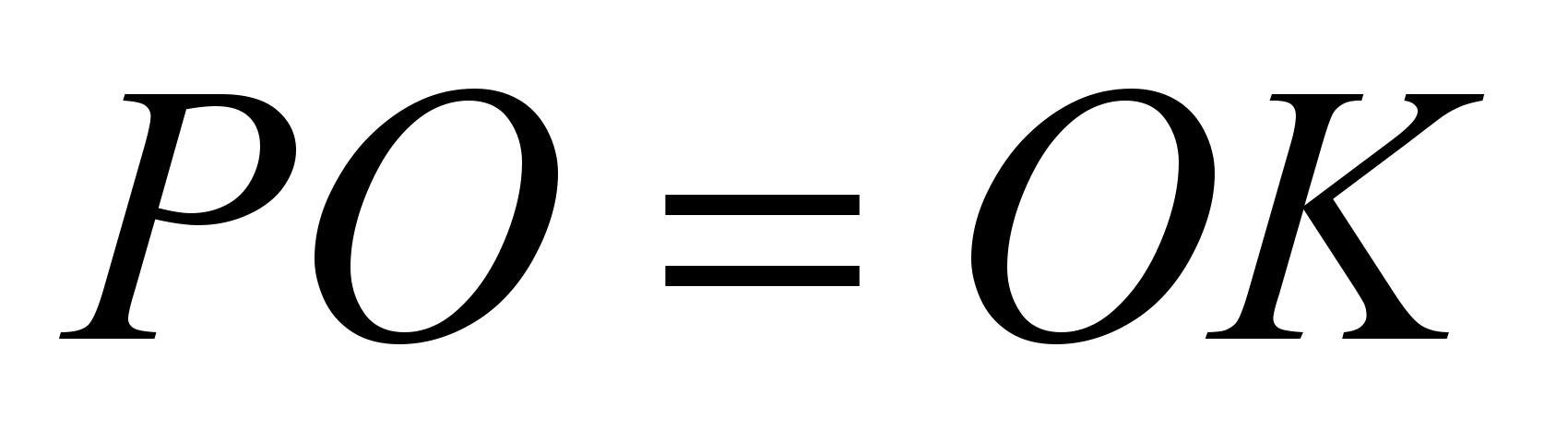و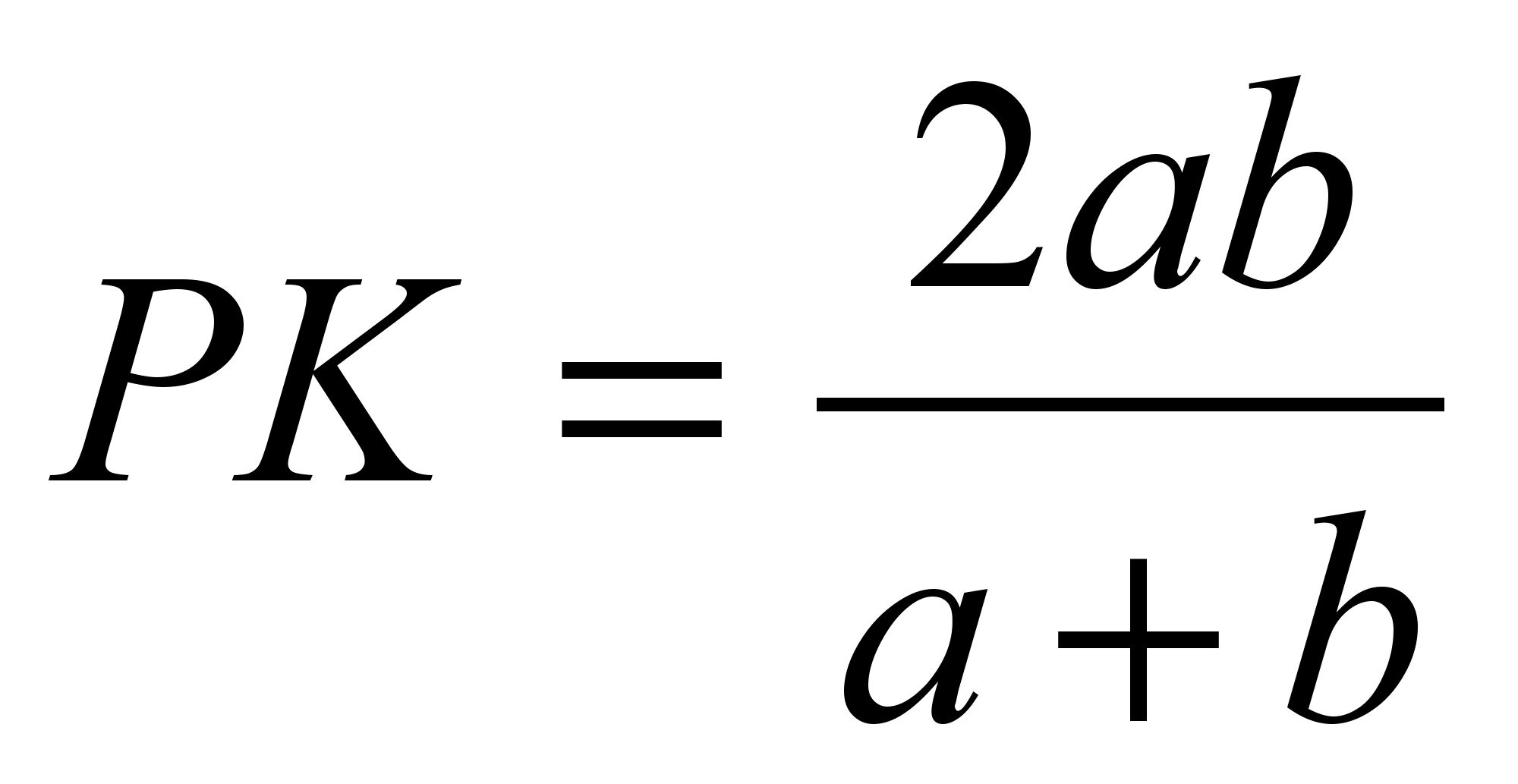

.

ما دانش‌آموزان را وادار می‌کنیم که به ویژگی ثابت شده پی ببرند: یک بخش به موازات پایه‌های ذوزنقه که از نقطه تقاطع مورب‌ها عبور می‌کند و دو نقطه را در طرفین به هم وصل می‌کند، با نقطه تقاطع مورب‌ها به نصف تقسیم می‌شود. طول آن میانگین هارمونیک پایه های ذوزنقه است.

بعدی از خاصیت چهار نقطه:در یک ذوزنقه، نقطه تقاطع مورب ها، نقطه تقاطع ادامه اضلاع، نقاط وسط پایه های ذوزنقه روی یک خط قرار دارند.

با آشنایی دانش‌آموزان با شباهت شکل‌ها (نه مثلث)، می‌توانیم طول بخشی را که ذوزنقه را به دو قسمت مشابه تقسیم می‌کند، پیدا کنیم.

به این ترتیب، قطعه ای که یک ذوزنقه را به دو ذوزنقه مشابه تقسیم می کند، طولی برابر با میانگین هندسی طول پایه ها دارد.

پس از استخراج فرمول مساحت ذوزنقه، اثبات آن مفید است ویژگی قطعه ای که ذوزنقه را به دو ناحیه مساوی تقسیم می کند.

بیایید یک سیستم بسازیم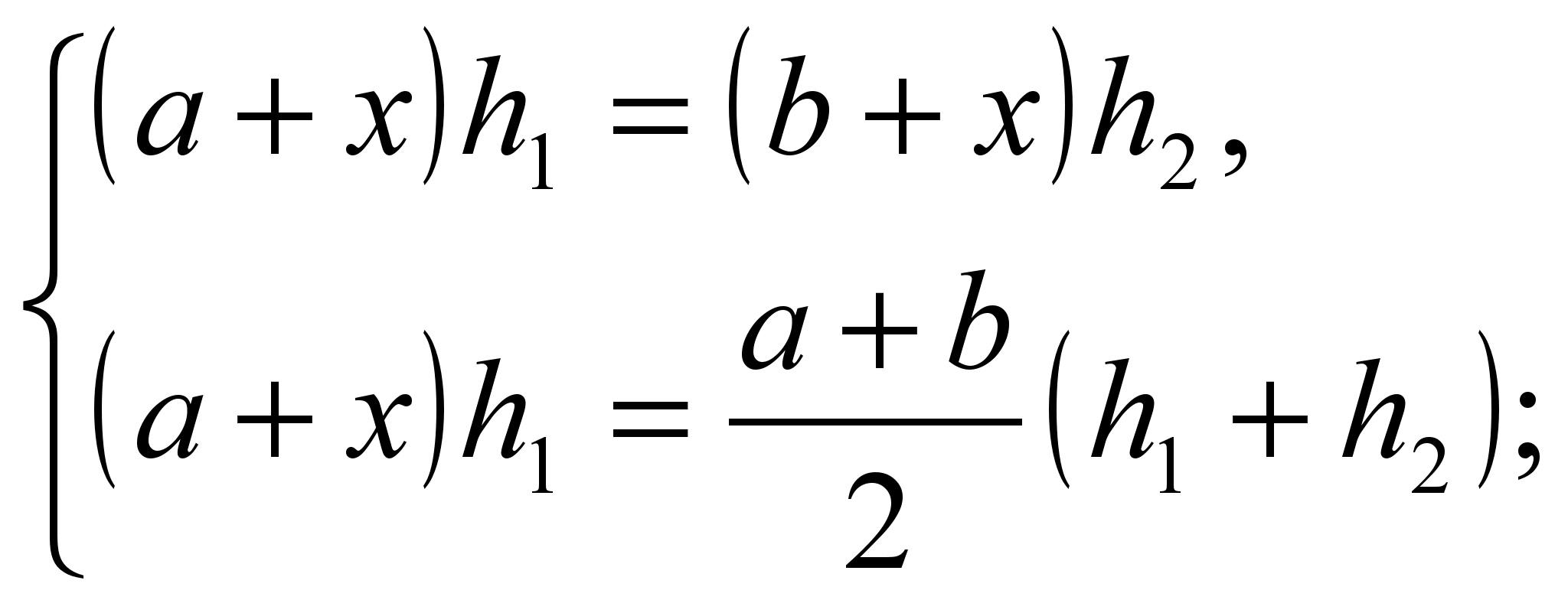

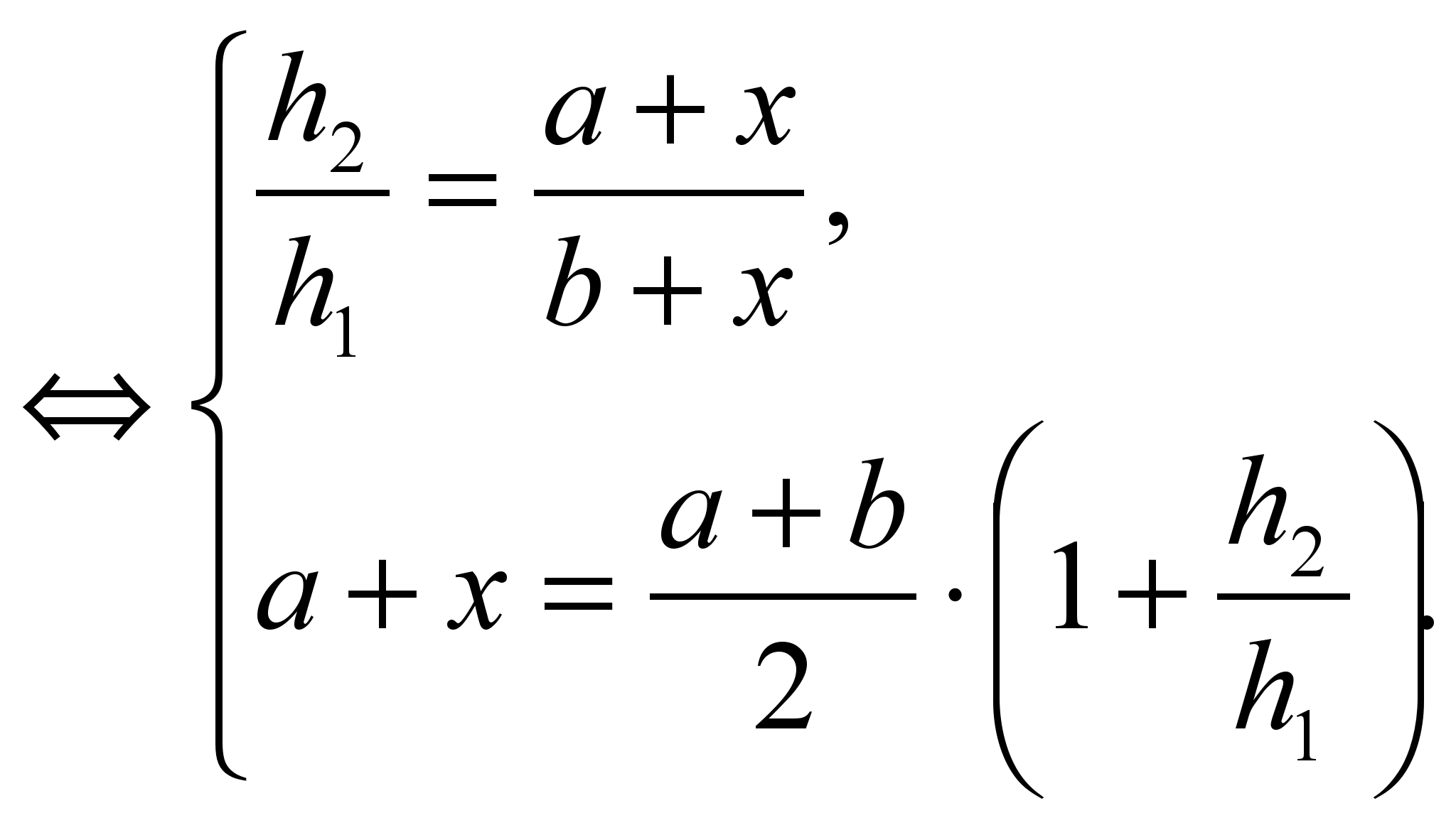
راه حل سیستم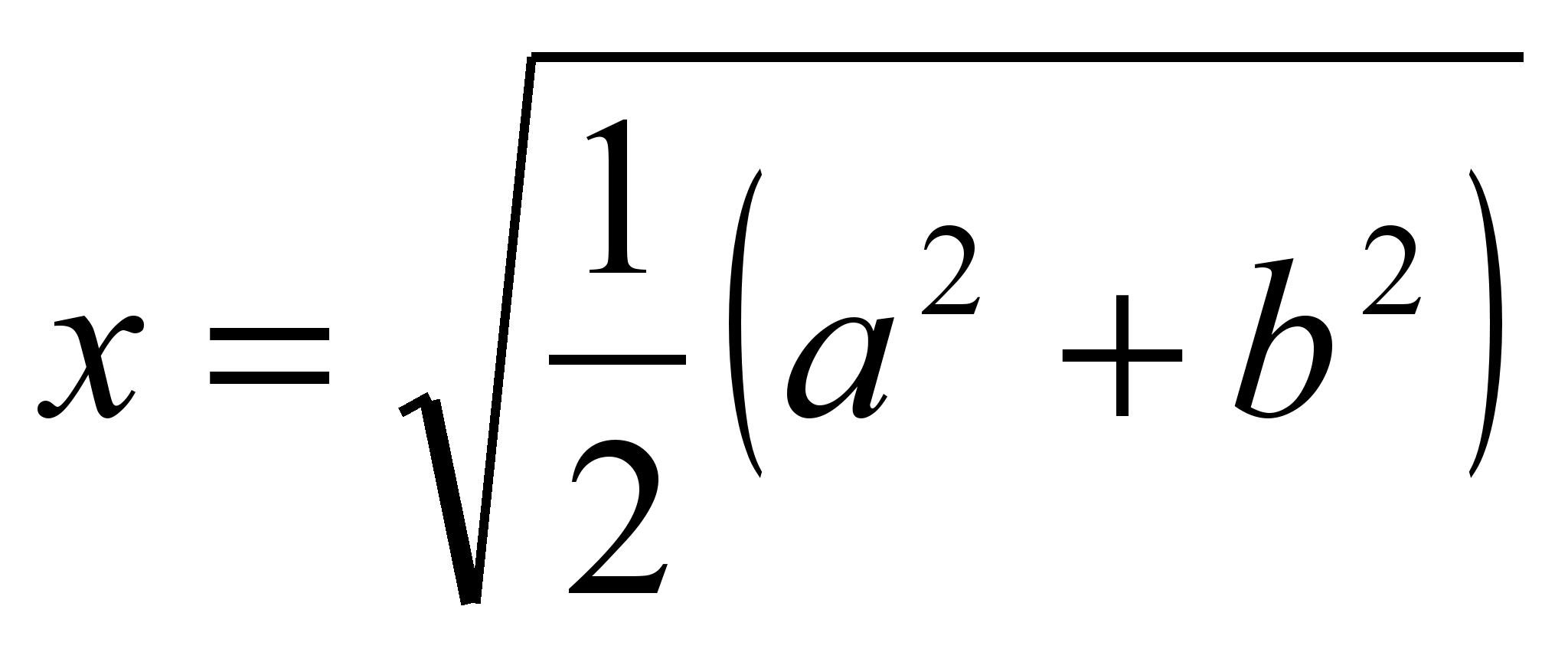

.

به این ترتیب، طول قطعه ای که ذوزنقه را به دو قسمت مساوی تقسیم می کند برابر است ب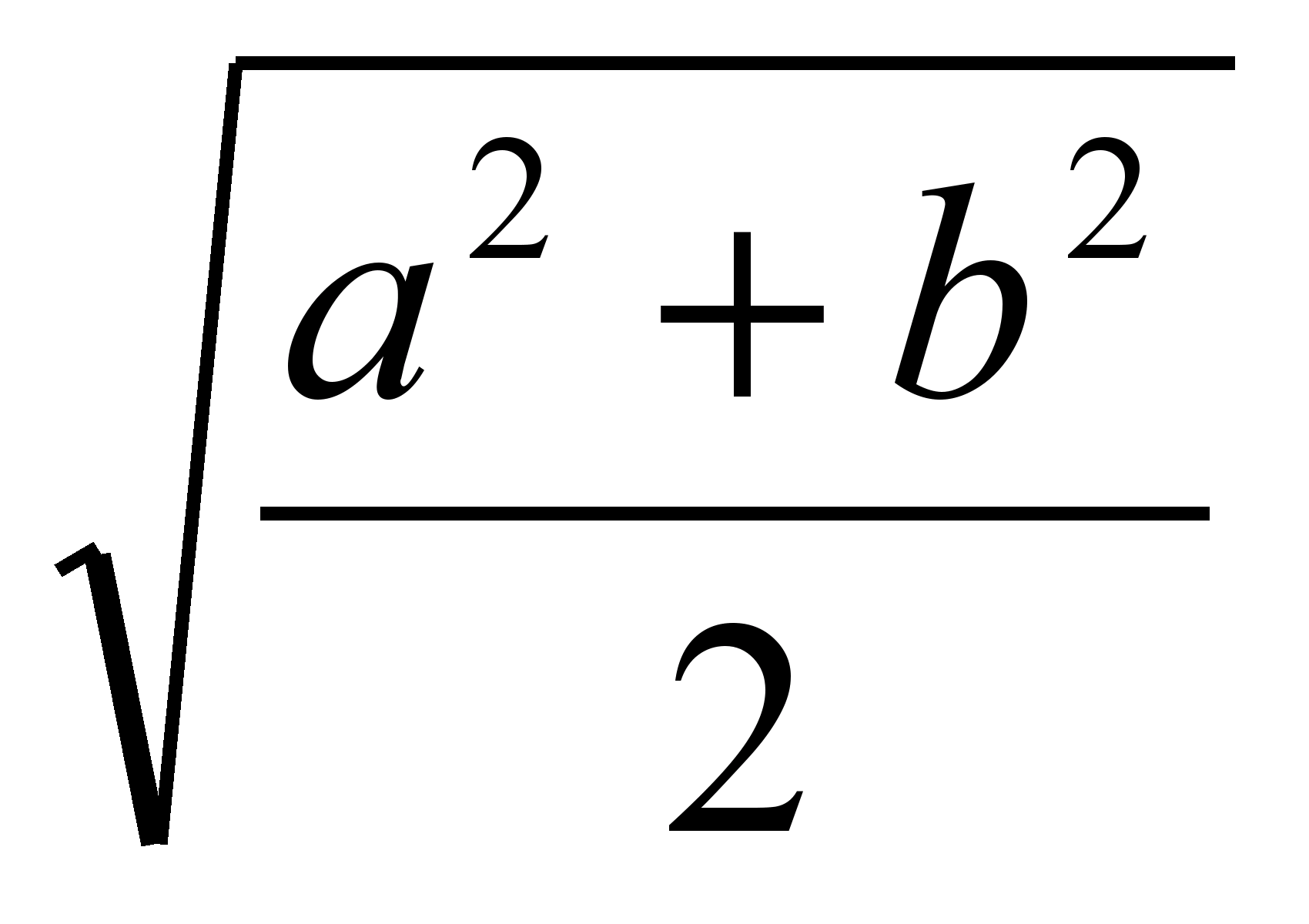ا

(ریشه میانگین طول مربع پایه ها). ).

برای اینکه دانش آموزان به ارتباط بین بخش های مشخص شده پی ببرند، باید از آنها خواسته شود که آنها را برای ذوزنقه معین بسازند. دانش آموزان بدون مشکل خط وسط ذوزنقه و پاره ای را می سازند که از نقطه تقاطع مورب های ذوزنقه موازی با پایه ها می گذرد. بخش سوم و چهارم کجا قرار خواهد گرفت؟ پاسخ به این سوال باید دانش آموزان را به کشف رابطه بین میانگین ها سوق دهد.

ویژگی و ویژگی یک چهار ضلعی محاطی و محصور باید برای تمام چهار ضلعی های شناخته شده برای دانش آموزان از جمله ذوزنقه مشخص شود.

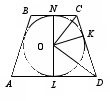
خواص ذوزنقه توصیف شده.ذوزنقه را می توان در مورد یک دایره توصیف کرد اگر و تنها در صورتی که مجموع طول پایه ها برابر با مجموع طول اضلاع باشد.

اولی واضح است. برای اثبات نتیجه دوم، باید مشخص شود که زاویه CODمستقیم، که آن هم مشکل بزرگی نیست. اما آگاهی از این پیامد به ما این امکان را می دهد که از مثلث قائم الزاویه در حل مسائل استفاده کنیم.

اجازه دهید عواقب آن را مشخص کنیم ذوزنقه متساوی الساقین محدود شده :

ارتفاع یک ذوزنقه متساوی الساقین محدود شده، میانگین هندسی قاعده ذوزنقه است. .

اصول اساسی روش شناسی برای مطالعه خواص ذوزنقه را در نظر بگیرید.

اول، استفاده است رویکرد وظیفه . نیازی به معرفی خصوصیات جدید ذوزنقه در درس هندسه نظری نیست. این ویژگی ها توسط دانش آموزان از طریق حل مسئله (بهتر از سیستم های مسئله) کشف و فرموله می شود. مهم این است که معلم بداند چه وظایفی و در چه نقطه ای باید تعیین شود. فرآیند آموزشی. علاوه بر این، هر ویژگی می تواند یک وظیفه کلیدی در سیستم وظیفه باشد.

ثانیاً سازمان "مارپیچی" مطالعه خواص ذوزنقه . می توانید چندین بار به ویژگی های فردی بازگردید، سپس این احتمال وجود دارد که دانش آموزان آنها را به خاطر بسپارند. مثلاً با مطالعه شباهت و سپس استفاده از بردارها می توان خاصیت چهار نقطه را اثبات کرد. مساحت مساوی مثلث های مجاور اضلاع ذوزنقه را می توان با استفاده از ویژگی مثلث هایی با ارتفاع مساوی که به اضلاع روی یک خط کشیده شده اند و فرمول ثابت کرد.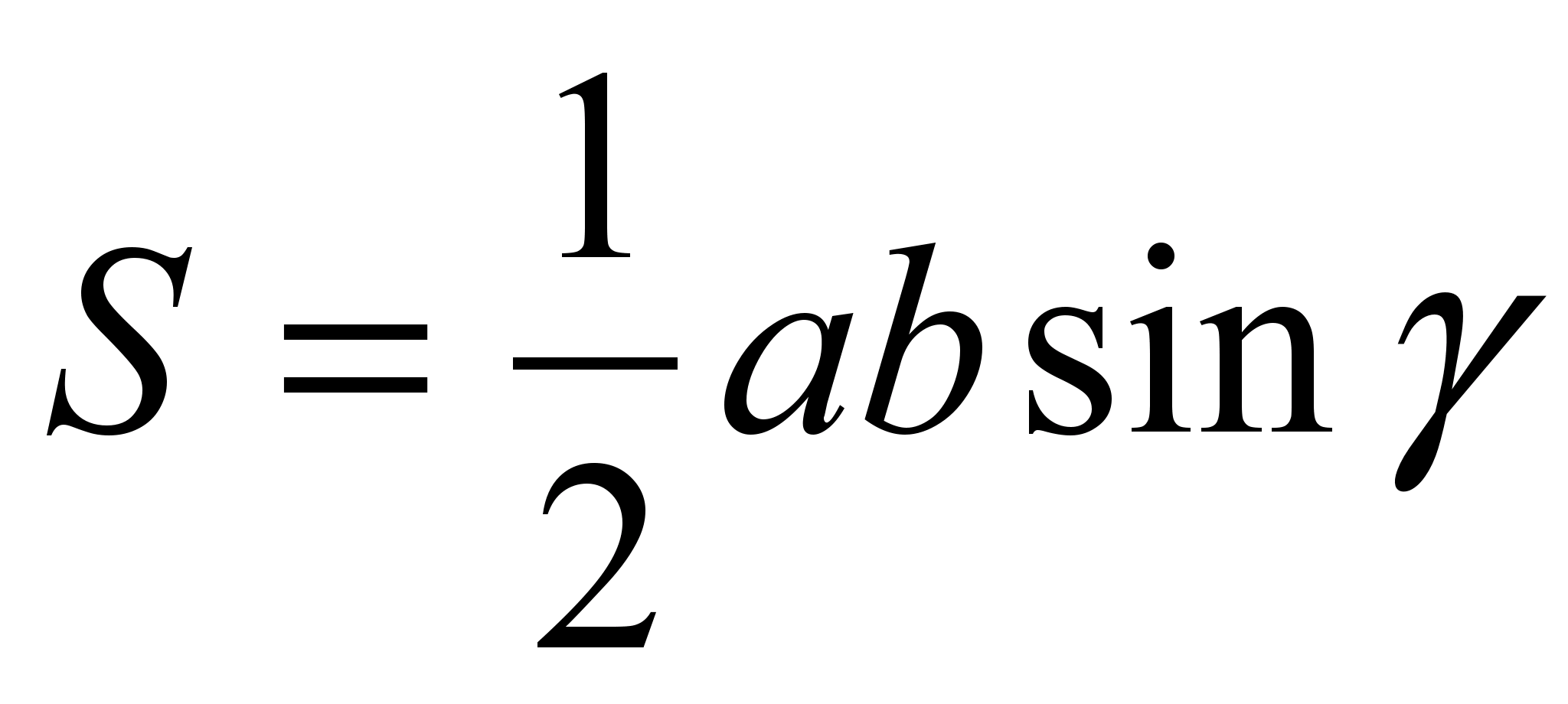

. شما می توانید خواص مثلث قائم الزاویه را در ذوزنقه محاط شده، قضیه سینوس در ذوزنقه محاط شده و غیره را محاسبه کنید.

پیشنهاد گنجاندن ویژگی های "غیر نرم افزاری" ذوزنقه در محتوا دوره مدرسههندسه، فناوری کار برای مطالعه آنها، اشاره مکرر به خواص ذوزنقه در هنگام مطالعه موضوعات دیگر به دانش آموزان امکان می دهد تا ذوزنقه را عمیق تر درک کنند و موفقیت حل مسائل را در کاربرد خواص آن تضمین کنند.
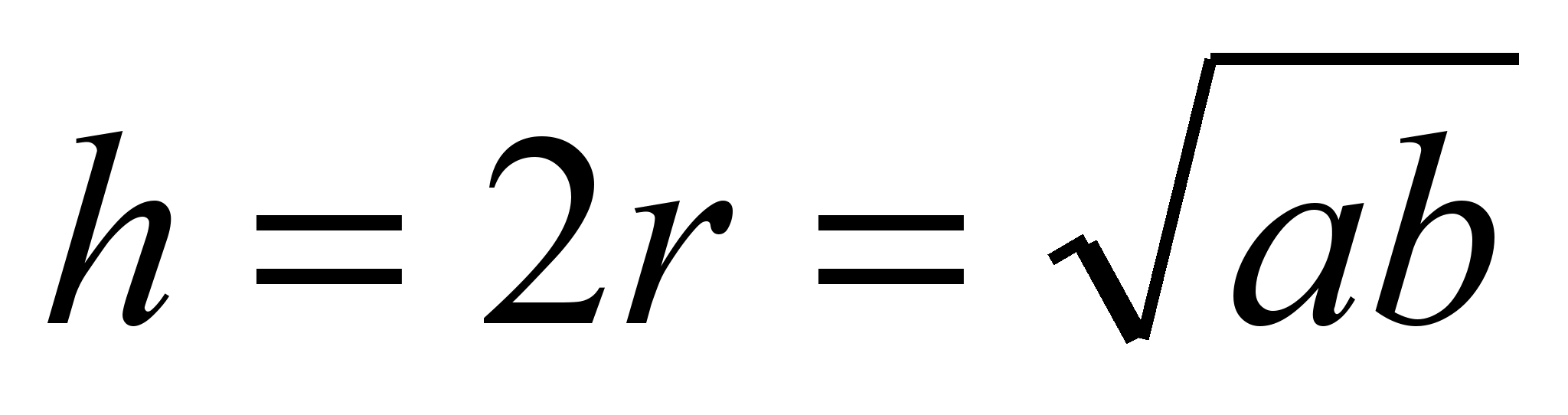